자연어처리-1 피드 포워드 신경망 언어모델(NNLM)

피드 포워드 신경망

순방향 신경망이라고도 하며, 일반적인 신경망을 피드 포워드 신경망이라고 한다.
딥러닝에서의 피드 포워드란, 입력층으로 데이터가 들어오고, 1개 이상의 은닉층을 거쳐서 일련의 가중치를 통해 출력층으로 직접 feed되는 것을 말한다.

N-gram 언어모델

피드 포워드 신경망 언어모델이 나오기 전에는 NLP분야에서 통계적인 방법을 사용하였다.
대표적인 통계적 언어모델(SLM)인 N-gram 언어모델은 일부 단어(N)만 고려하는 접근 방법을 사용한다.
개념만 대충 설명하자면, 만약 ‘what will the fat cat sit __‘ 이라는 문장이 있고, N이 4일때, __을 예측하는 문제라면, sit 다음에 올 단어를 예측한는 것은 n-1에 해당하는 앞의 3개 단어인 fat cat sit 만으로 조건부 확률을 구해서 통계를 내는 방식이다.
N-gram 모델의 한계가 있는데, 앞의 단어 몇개만 참고하다 보니, 의도하고 싶은 대로 문장이 나오지 않는 희소성 문제가 있다. 또한 N을 어떻게 설정해야 되는지의 문제가 있다.

자세한 설명은 여기로 가면 된다.

NNLM

N-gram 언어모델의 단점을 해결하기 위해서 나온 것이 NNLM이다. NNLM은 N-gram 언어모델에서 희소성 문제를 해결한 모델이다.
희소성을 해결하려면 단어의 의미적 유사성을 학습할 수 있도록 설계해야 하는데, 이 아이디어는 단어의 벡터 간 유사도를 구할 수 있는 벡터를 얻어내는 워드 임베딩을 통해 해결하였다.
이제 NNLM이 훈련을 통해 어떻게 워드 임베딩을 구할 수 있는지 알아보자.

NNLM모델 구조

모든 NLP분야에서는 문장을 원-핫 벡터로 만들어야 한다. 그 이유는 다들 알것이다. 모델의 입력으로 문자열을 직접적으로 줄 수 없기 때문이다. ‘what will the fat cat sit on’ 이라는 문장이 있을 때, 원-핫 벡터는 이렇게 만들 수 있다.

what = [1, 0, 0, 0, 0, 0, 0]
will = [0, 1, 0, 0, 0, 0, 0]
the = [0, 0, 1, 0, 0, 0, 0]
fat = [0, 0, 0, 1, 0, 0, 0]
cat = [0, 0, 0, 0, 1, 0, 0]
sit = [0, 0, 0, 0, 0, 1, 0]
on = [0, 0, 0, 0, 0, 0, 1]

여기서 단어 단위로 쪼개진 값들을 흔히 토큰이라고 한다.
이 원-핫 벡터들이 훈련을 위한 입력이면서, 동시에 예측을 위한 레이블이 된다.
NNLM은 N-gram모델 처럼 모든 단어를 참고하는게 아니라, 정해진 개수만큼 참고한다.
예시로 ‘the fat cat sit’ 의 4개의 단어(N이아니라 Window라고 부름)를 참고해서 ‘on’을 예측하는 모델의 구조를 한번 보자.

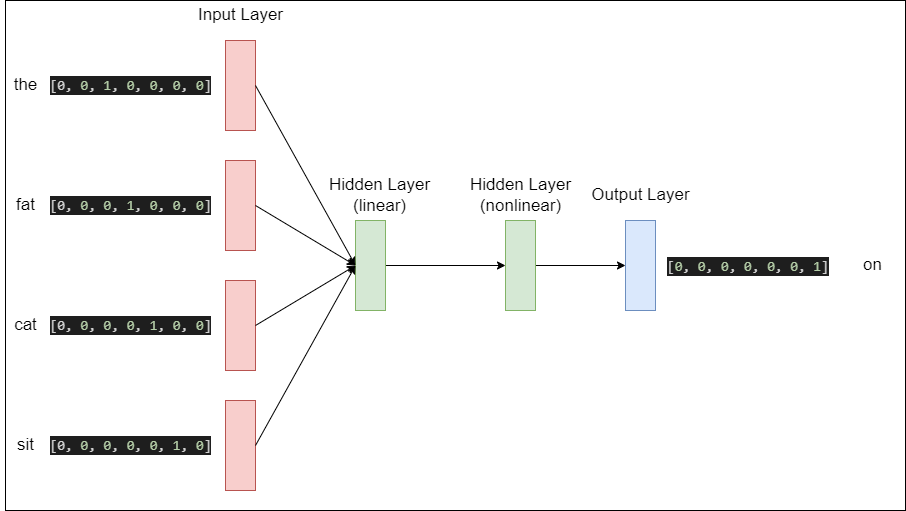
4개의 원-핫 벡터를 입력으로 넣어서 두개의 은닉층을 지나 ‘sit’의 원-핫 벡터를 예측하는 모델이다. output의 원-핫 벡터는 모델이 예측한 값의 오차를 구하기 위한 레이블로 사용된다. 그리고 오차로부터 손실 함수를 사용하여 학습하게 된다.

Linear Hidden Layer

Input Layer를 지나면 은닉층을 만난다. 이 은닉층은 신기하게도 비선형구조가 아니라 선형구조이다. 가중치 행렬과의 곱셈은 이루어 지지만 활성화 함수가 없기 때문에, 값이 계산된 값이 그대로 다음 은닉층으로 넘어가게된다.
은닉층의 크기를 M으로 설정하면, 각 입력 단어들은 투사층에서 V × M 크기의 가중치 행렬과 곱해진다. 여기서 V는 원-핫 벡터의 크기를 의미한다. 만약 원-핫 벡터의 차원이 7이고, M이 5라면 가중치 행렬 W는 7 × 5 행렬이 된다. 계산이 어떻게 이루어지는지 한번 보자.

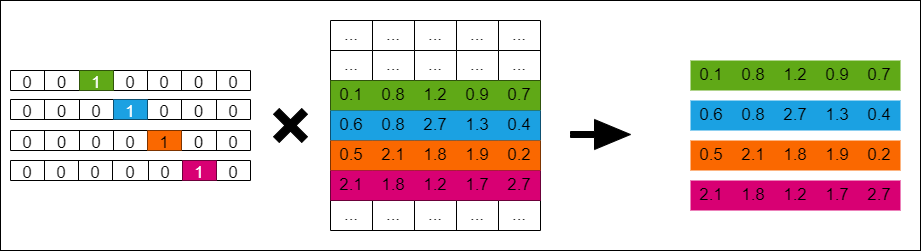
원-핫 벡터의 특성으로 인해서 원-핫 벡터와 가중치 행렬의 곱은 그냥 W의 원-핫 벡터의 인덱스행을 그대로 가져온 것과 같다. np.dot()을 이용해서 출력해보면 이해가 갈 것이다.

import numpy as np
one_hot_vec = np.array([0, 0, 0, 1, 0, 0, 0])
W = np.random.randn(7, 5)
print(W)
np.dot(one_hot_vec, W)

[[ 1.03170811  1.09242654 -1.28536347  1.37316217  1.08854411]
 [ 0.90589407 -0.76318408 -1.37341595 -0.32998329 -0.63924971]
 [ 0.89832282 -2.1964927   0.28666672 -1.00973592  1.14388714]
 [ 0.72534891  0.80296724 -0.0444068   0.61365572  0.70141869]
 [ 0.44535133 -0.04081508  0.85096525  0.95486399  1.67836364]
 [ 0.42064528 -0.12183989  0.1124817  -0.59734816  0.26549582]
 [ 0.61191261 -0.58559681 -0.83964374  0.37248946 -0.00617631]]


array([ 0.72534891,  0.80296724, -0.0444068 ,  0.61365572,  0.70141869])

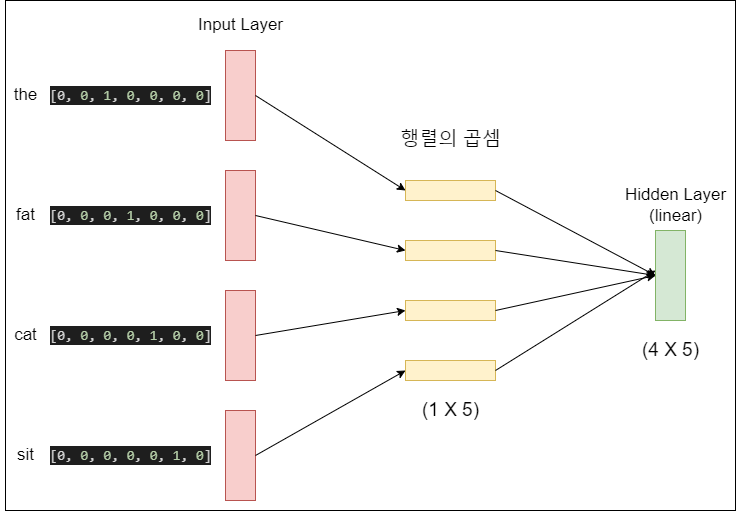
값을 계산한 후에 V차원 이었던 원-핫 벡터는 M차원의 벡터로 매핑된다. 즉, 7차원이었던 벡터가 5차원으로 변경된다. 이 벡터들은 초기에는 랜덤값을 가지지만 학습 과정에서 값이 계속 변경되는데 이를 임베딩 벡터라고 한다. 이 값들이 하나로 합쳐져서 은닉층으로 들어가게 된다. 따라서 은닉층은 N * M 형태인 4 * 5 형태가 된다.

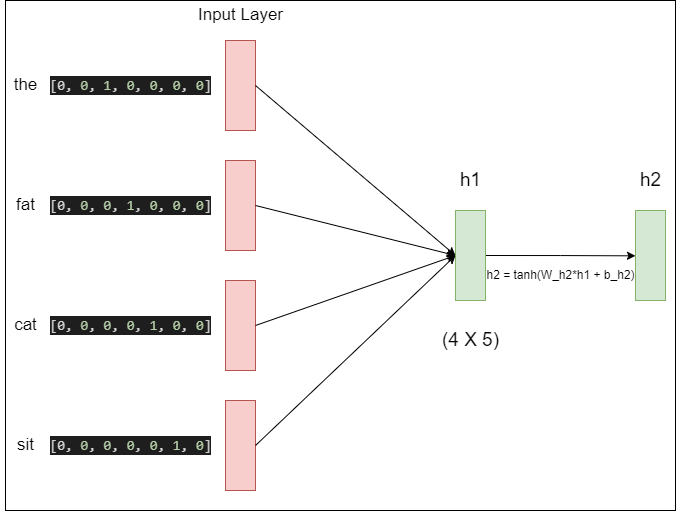
NonLinear Hidden Layer

첫번째 은닉층에서의 결과는 h의 크기를 가지는 은닉층을 지나게 된다. 일반적인 피드 포워드 신경망에서 은닉층을 지난다는 것은 은닉층의 입력으로 가중치가 곱해진 후 편향이 더해져서 활성화 함수의 입력이 된다. 첫번째 은닉층을 h1 두번째 은닉층을 h2라고 할 때, 계산식은 $h2 = tanh(W_{h2*h1} + b_{h1})$가 된다.

Output Layer

두번째 은닉층의 출력은 활성화 함수 tanh의 계산과 함께 V의 크기를 가지는 출력층으로 향한다. 이 과정에서 또다른 가중치와 곱해지고 편향이 더해지면, 5차원이었던 벡터가 V차원의 벡터를 얻게 된다. 왜 이런지 모르겠다면, 행렬의 곱셈을 찾아보자.
출력층에서는 활성화 함수로 softmax를 사용하는데, V차원의 벡터는 softmax 함수를 지나면서 0과 1사이의 실수값을 가지는 확률로 표현이 된다. 이 벡터를 $\hat{y}$ 이라고 할때, 수식으로 표현하면
$\hat{y} = softmax(W_{y*h2} + b_y)$ 로 표현할 수 있다.

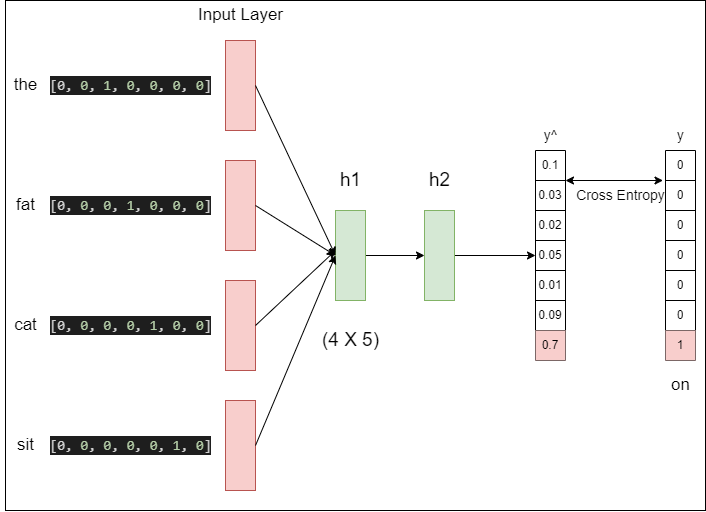
위 그림에서 볼 수 있듯이, $\hat{y}$의 값은 다음 단어일 확률을 나타낸다. 그리고 실제값 $y$의 값에 가까워 져야 한다. 이 두 벡터의 값을 가까워지게 하기 위해서 손실함수로 크로스 엔트로피 함수를 사용한다.
역전파가 이루어 지면 모든 가중치 행렬들이 학습되는데, 여기에서 첫번째 은닉층에서의 가중치 행렬도 포함되어 있으므로 임베딩 벡터값 또한 학습된다.
이렇게 학습된 임베딩 벡터는 훈련이 끝난 후, 다음 단어를 예측하는 과정에서 단어의 유사도가 없더라도, 예측을 할 수 있게 된다.
결국 NNLM도 지도학습의 한 분야이며, 정답과 예측의 오차값을 계산하여 최소화 하는 방향으로 가중치와 편향이 학습된다.

NNLM의 장점과 단점

NNLM을 사용하므로써 기존 N-gram 모델에서의 단점인 단어의 유사도를 계산할 수 있게 되었다.
하지만 N-gram 모델에서와 마찬가지로 다음 단어를 예측하기 위해 정해진 N개의 단어만을 참고 할 수 있다는것이 단점이다. 이 단점을 극복한 모델이 RNN(순환신경망)이다.