딥러닝 역전파

역전파(Back propagation)란?

신경망을 학습시키기 위한 순전파의 반대 개념이다. 순전파랑은 다르게 뒤에서부터 계산하기 때문에 역전파라고 한다. t의 값과 실제 모델이 계산한 y의 오차를 구한 후 오차값을 다시 뒤로 전파해가면서 각 노드들의 매개변수들을 갱신한다.

함성함수의 미분(Chain rule)

고등학교 수학시간에 배운 합성함수의 미분이 등장한다. 대략적인 정의는

함성 함수의 미분은 합성 함수를 구성하는 각 함수의 미분의 곱으로 나타 낼 수 있다

예를 들어서 $z = (x+y)^2$ 라는 식이 있다고 할 때, $(x+y)$를 $t$라고 놓으면 식은 $z = t^2$ , $t = (x+y)$ 처럼 두개로 정의할 수 있다. 여기서 $\partial z \over \partial x$(x에 대한 z의 미분)은 $\partial z \over \partial t$(t에 대한 z의 미분)과 $\partial t \over \partial x$(x에 대한 t의 미분)의 곱으로 나타낼 수 있다는 것이다.

$\partial z \over \partial x$ = $\partial z \over \partial t$ $\partial t \over \partial x$

참고로 위 식을 계산하면 $2(x+y)$가 된다.

역전파 구현

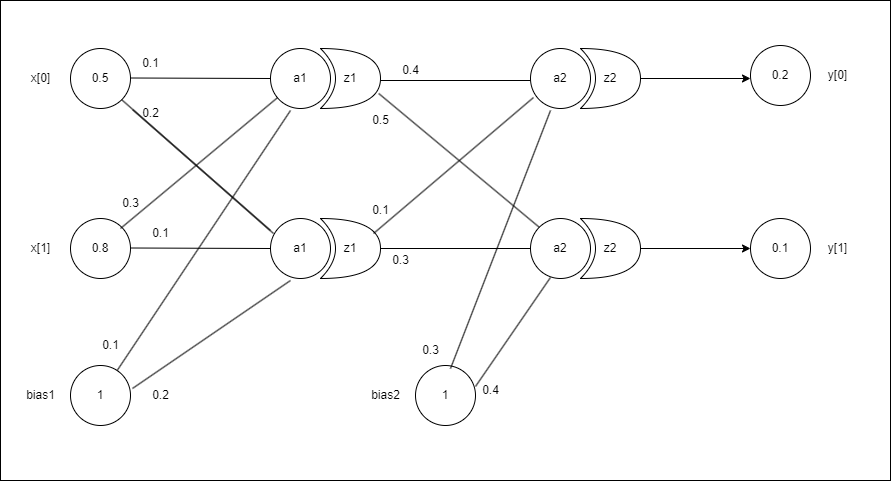
예제로 사용할 신경망의 구조는 전에 포스팅 했던 순전파 구조와 같다. 순전파와는 조금 다른 점은 역전파를 조금 더 쉽게 계산하기 위해 각 층마다 나온 결과값을 추가하고 편향 값은 삭제하였다.

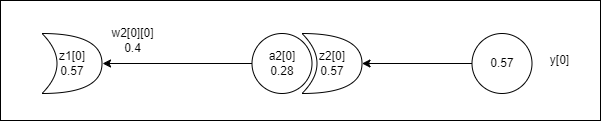
원래 $E$는 $1 \over n$ $\displaystyle\sum_{i=0}^{n}{(t_i-y_i)^2}$ 인데 여기서 $n=2$ (출력이 2개이기 때문)이고 $y[0]$ 에 대한 에러만 구하면 된다. 그럼 하나씩 구해보자. $z2[0]$ 에 대한 편미분이므로 $t_0$ 는 무시하고 계산한다.
$\partial E \over \partial z2[0]$ = $1 \over 2$$(t_0 - z2[0])^2$ = $(t_0 - z2[0]) * -1$ = $(0.2 - 0.57) * -1$ = $0.37$ 이 나오게 된다. 이는 에러$E$에 대해서 $z2[0]$이 $0.37$만큼 기여 했다는 뜻이 된다.
$\partial z2[0] \over \partial a2[0]$ = $z2[0] * (1 - z2[0])$ = $0.57 * (1-0.57)$ = $0.25$

이 계산은 sigmoid의 미분이므로 맨 밑에서 자세하게 설명하겠다.

$\partial a2[0] \over \partial w2_{0,0}$ = $z1[0] + 0$ = $0.57$

$z1[0] + 0$ 에서 0 은 편향이 없으므로 0이다.

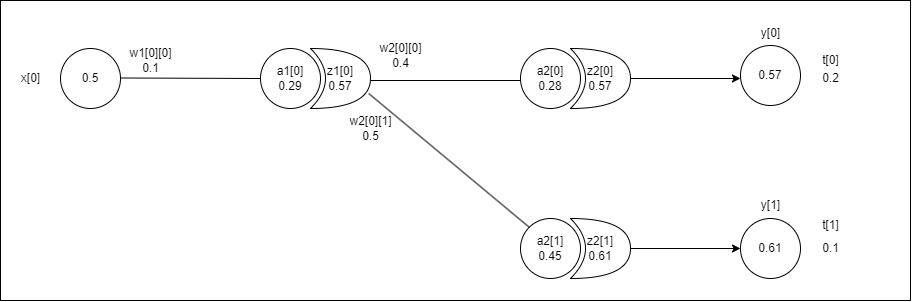
LaTex 수식이 너무 복잡해서 틀린것이 있을수 있습니다. Mathjax 버전문제로 수식이 적용되지 않아 사진으로 대체합니다. 죄송합니다 ㅠ

코드 구현

각 가중치 마다 직접 계산하였기 때문에 조금 복잡하실수도 있습니다!

def weight2_00(y, t):
    diff_loss = (t[0] - y[0]) * -1
    diff_sigmoid = y[0] * (1- y[0])
    diff_weight = z1[0] + 0
    weight = diff_loss * diff_sigmoid * diff_weight
    update_weight = w2[0][0] - (lr * weight)
    return update_weight

def weight2_01(y, t):
    diff_loss = (t[1] - y[1]) * -1
    diff_sigmoid = y[1] * (1 - y[1])
    diff_weight = z1[0] + 0
    weight = diff_loss * diff_sigmoid * diff_weight
    update_weight = w2[0][1] - (lr * weight)
    return update_weight

def weight1_00(y, t):
    # loss1
    diff_loss1 = (t[0] - y[0]) * -1
    diff_sigmoid1 = y[0] * (1- y[0])
    diff_weight1 = w2[0][0]
    loss1 = diff_loss1 * diff_sigmoid1 * diff_weight1
    # loss2
    diff_loss2 = (t[1] - y[1]) * -1
    diff_sigmoid2 = y[1] * (1 - y[1])
    diff_weight2 = w2[0][1]
    loss2 = diff_loss2 + diff_sigmoid2 + diff_weight2
    # weight
    diff_sigmoid = z1[0] * (1 - z1[0])
    diff_weight = x[0]
    weight = (loss1 + loss2) * diff_sigmoid * diff_weight
    update_weight = w1[0][0] - (lr * weight)
    return update_weight

def weight1_10(y, t):
    # loss1
    diff_loss1 = (t[0] - y[0]) * -1
    diff_sigmoid1 = y[0] * (1- y[0])
    diff_weight1 = w2[0][0]
    loss1 = diff_loss1 * diff_sigmoid1 * diff_weight1
    # loss2
    diff_loss2 = (t[1] - y[1]) * -1
    diff_sigmoid2 = y[1] * (1 - y[1])
    diff_weight2 = w2[0][1]
    loss2 = diff_loss2 + diff_sigmoid2 + diff_weight2
    # weight
    diff_sigmoid = z1[0] * (1 - z1[0])
    diff_weight = x[1]
    weight = (loss1 + loss2) * diff_sigmoid * diff_weight
    update_weight = w1[1][0] - (lr * weight)
    return update_weight

def weight2_11(y, t):
    diff_loss = (t[1] - y[1]) * -1
    diff_sigmoid = y[1] * (1- y[1])
    diff_weight = z1[1] + 0
    weight = diff_loss * diff_sigmoid * diff_weight
    update_weight = w2[1][1] - (lr * weight)
    return update_weight

def weight2_10(y, t):
    diff_loss = (t[0] - y[0]) * -1
    diff_sigmoid = y[0] * (1- y[0])
    diff_weight = z1[1] + 0
    weight = diff_loss * diff_sigmoid * diff_weight
    update_weight = w2[1][0] - (lr * weight)
    return update_weight

def weight1_11(y, t):
    # loss1
    diff_loss1 = (t[1] - y[1]) * -1
    diff_sigmoid1 = y[1] * (1- y[1])
    diff_weight1 = w2[1][1]
    loss1 = diff_loss1 * diff_sigmoid1 * diff_weight1
    # loss2
    diff_loss2 = (t[0] - y[0]) * -1
    diff_sigmoid2 = y[0] * (1 - y[0])
    diff_weight2 = w2[1][0]
    loss2 = diff_loss2 + diff_sigmoid2 + diff_weight2
    # weight
    diff_sigmoid = z1[1] * (1 - z1[1])
    diff_weight = x[1]
    weight = (loss1 + loss2) * diff_sigmoid * diff_weight
    update_weight = w1[1][1] - (lr * weight)
    return update_weight

def weight1_01(y, t):
    # loss1
    diff_loss1 = (t[1] - y[1]) * -1
    diff_sigmoid1 = y[1] * (1- y[1])
    diff_weight1 = w2[1][1]
    loss1 = diff_loss1 * diff_sigmoid1 * diff_weight1
    # loss2
    diff_loss2 = (t[0] - y[0]) * -1
    diff_sigmoid2 = y[0] * (1 - y[0])
    diff_weight2 = w2[1][0]
    loss2 = diff_loss2 + diff_sigmoid2 + diff_weight2
    # weight
    diff_sigmoid = z1[0] * (1 - z1[0])
    diff_weight = x[0]
    weight = (loss1 + loss2) * diff_sigmoid * diff_weight
    update_weight = w1[0][1] - (lr * weight)
    return update_weight

아래 코드는 역전파로 1500회 반복후 100번 마다 예측값과 손실값을 출력했습니다

for i in range(1500):
    a1 = np.dot(x, w1)
    z1 = sigmoid(a1)
    a2 = np.dot(z1, w2)
    z2 = sigmoid(a2)
    y = z2
    w1[0][0] = weight1_00(y, t)
    w1[0][1] = weight1_01(y, t)
    w1[1][0] = weight1_10(y, t)
    w1[1][1] = weight1_11(y, t)
    w2[0][0] = weight2_00(y, t)
    w2[0][1] = weight2_01(y, t)
    w2[1][0] = weight2_10(y, t)
    w2[1][1] = weight2_11(y, t)
    def MSE(y, t):
        return ((y-t)**2).mean(axis=None)
    loss = MSE(y,t)
    if i%100 == 0:
        print(f"[{i}] 예측: {y}, 손실: {loss}")

[0] 예측: [0.57035173 0.61051125], 손실: 0.19889106944011697
[100] 예측: [0.4652094  0.46179414], 손실: 0.10061551430383414
[200] 예측: [0.30316578 0.26389535], 손실: 0.018752432278208896
[300] 예측: [0.21567796 0.1543594 ], 손실: 0.0016003711407895623
[400] 예측: [0.20359713 0.13133002], 손실: 0.000497254753525437
[500] 예측: [0.20047112 0.12055811], 손실: 0.00021142898257934023
[600] 예측: [0.1996288  0.11425606], 손실: 0.0001016864486579869
[700] 예측: [0.19947258 0.11017801], 손실: 5.193500634542015e-05
[800] 예측: [0.19951067 0.10738099], 손실: 2.73592508642205e-05
[900] 예측: [0.19958301 0.1053845 ], 손실: 1.4583376980820222e-05
[1000] 예측: [0.19963875 0.10391061], 손실: 7.711680501901155e-06
[1100] 예측: [0.19966144 0.10278082], 손실: 3.923785776709175e-06
[1200] 예측: [0.19964131 0.10186601], 손실: 1.8053327204324974e-06
[1300] 예측: [0.19956184 0.10105443], 손실: 6.519032415677173e-07
[1400] 예측: [0.1993869  0.10021984], 손실: 2.1211354969700546e-07

sigmoid함수의 미분

$d \over dx$ $sigmoid(x)$ = $d \over dx$ $(1+e^{-x})^{-1}$
= $(-1)$ ${1 \over (1+e^{-x})^2}$ $d \over dx$ $(1+e^{-x})$
= $(-1)$ ${1 \over (1+e^{-x})^2}$ $(0 + e^{-x})$ $d \over dx$ $(-x)$
= $(-1)$ ${1 \over (1+e^{-x})^2}$ $e^{-x}$ $(-1)$
= $e^{-x} \over (1+e^{-x})^2$
= $1+e^{-x}-1 \over (1+e^{-x})^2$
= $(1+e^{-x}) \over (1+e^{-x})^2$ - $1 \over (1+e^{-x})^2$
= $1 \over 1+e^{-x}$ - $1 \over (1+e^{-x})^2$
= $1 \over 1+e^{-x}$ $(1-$ $1 \over 1+e^{=x}$ $)$
= $sigmoid(x)$$(1-sigmoid(x))$

오늘의 정리

1. 순전파를 이용해서 구할 때에는 3000번을 반복했지만 역전파를 이용하면 1500번 반복 만으로 좋은 결과를 얻을 수 있다.
2. 각 가중치마다 손실 값에 얼만큼 영향을 미치는지를 구하는데 이것은 chain rule로 구할 수 있다.

참고자료

1. sigmoid미분
2. 역전파
3. 밑바닥부터 시작하는 딥러닝