선형회귀 한번에 이해하기!

선형회귀란?

알 수 있는 데이터 값을 사용하여 알 수 없는 데이터의 값을 예측하는 분석 기법이다.
다른 변수의 값을 변하게 하는 변수를 $x$, 변수 $x$의 값에 의해서 값이 종속적으로 변하는 변수를 y라고 할 때, $x$를 독립변수, $y$를 종속변수 라고한다.
선형 회귀는 $x$와 $y$의 선형 관계를 모델링 하는 것이다. $x$가 1개라면 단순 선형 회귀라고 하고, $x$가 여러개라면 다중 선형 회귀 라고 한다.
엄청 쉽게 말하면 데이터를 가지고 그 데이터의 성질?을 잘 설명할 수 있는 선을 그리는 일을 말한다.

단순 선형 회귀

단순 선형 회귀의 수식은 $y = wx + b$ 로 나타낸다. 중학교 수학때 배운 1차 함수와 모양이 같다. 여기서 $w$는 가중치, $b$를 편향이라고 한다. $w$와 $b$에 따라 선의 모양이 무궁무진하기 때문에 그 데이터를 잘 설명하는 최고의 $w$와 $b$를 찾는 것이다.

다중 선형 회귀

다중 선형 회귀의 수식은 $y=w_1x_1+w_2x_2+…+w_nx_n+b$로 나타낸다. 단순 선형 회귀와는 달리 독립변수가 여러개 있는 구조이다. 독립변수가 여러개 있다는 것이 무슨 말일까? 간단하게 예를 들어보겠다.
주택가격을 예측한다고 가정하자. 여기서 독립변수는 단순히 집의 크기 뿐 아니라, 방의 개수, 인구밀도, 편의성 등등 많은 요인에 의한다. 때문에 독립변수가 여러개인 것이다.

손실 함수

앞에서 말했듯이 선형회귀는 선을 그리는 것이라고 얘기했었다.
선은 $w$와 $b$에 의해 그려지므로 데이터를 가장 잘 나타내는 최적의 $w$와 $b$를 찾아야 하는데, 여기서 실제값과 예측값의 오차를 계산하는 식을 손실 함수라고 한다.
손실함수는 단순히 실제값과 예측값에 대한 오차를 표현하면 되는 것이 아니고, 예측값의 오차를 줄이는 일에 최적화 된 식이어야 한다. 그 식 중 하나가 많이 사용하는 평균 제곱 오차(MSE)이다.

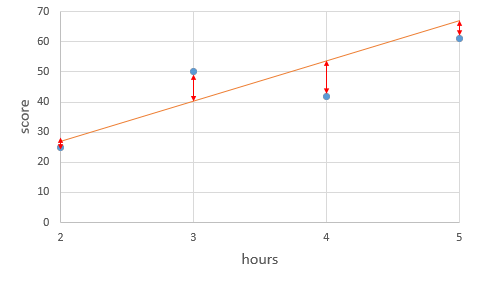
그림은 오차에 대한 예시를 나타낸다. 위 그림의 직선은 정답이 아니다. 점과 직선 사이의 거리(오차)를 손실 함수를 사용하여 줄여야 한다.
선형회귀의 목표는 모든 데이터로부터의 오차를 최소화 할 수 있는 최적의 기울기 $w$와 절편 $b$을 찾는 것이다.

경사하강법

그렇다면 머신러닝과 딥러닝에서의 오차는 무슨 방식으로 줄이는 것일까? 이때 사용되는 알고리즘을 옵티마이저 또는 최적화 알고리즘이라고 부른다.
이 옵티마이저를 통해 적절한 $w$와 $b$를 찾아내는 과정을 훈련 또는 학습이라고 한다.
그 중에서 경사하강법은 가장 기본적인 옵티마이저이다. 어려운 내용은 그냥 넘어가고 한 가지 알고가야 하는 사실은 기울기와 손실의 관계는 2차함수의 모양처럼 생겼다는 것이다.

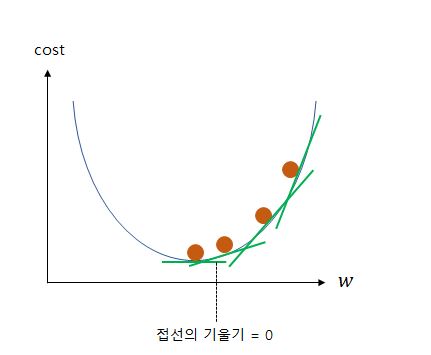
그림처럼 기울기 $w$가 무한대로 커지면 손실값 또한 무한대로 커지고, 반대로 기울기 $w$가 무한대로 작아져도 손실값은 무한대로 커진다.
손실값이 제일 작을 때에는 그래프의 볼록한 부분의 맨 아래 쪽이다.
기울기 $w$를 조금씩 변화시켜가면서 손실을 점점 줄여가는 방식으로 마지막에는 손실값이 제일 적은 기울기를 찾아가는 것이 경사하강법이다. 이 과정에서 미분이 사용된다.

학습률

학습률은 기울기 $w$의 값을 변경할 때, 얼마나 큰 폭으로 변경할지를 결정하는 변수이다.
학습률을 크게하면 최적의 $w$를 빠르게 찾을 수 있을 것 같지만 실제로는 오히려 $w$값이 발산해버린다.
반대로 학습률을 작게하면 학습 속도가 느려진다.
따라서 최적의 w를 찾기 위해서는 최적의 학습률을 찾는 것이 중요하다.

위의 설명은 절편 b를 배제하고 설명을 했지만 실제로는 w와 b에 대해서 동시에 경사하강법을 수행하면서 최적의 w와 b를 찾아낸다.
또한 풀고자하는 문제에 따라서 손실함수와 옵티마이저가 전부 다를수도 있기 때문에 적합한 방법을 찾아서 해결하는 것이 중요하다.