다중 선형회귀분석 실습

선형회귀를 모르시는 분들은 선형회귀 한번에 이해하기! 이 글을 참고해 주세요!

이번 시간에는 다중 선형회귀분석을 실시해 보도록 하자!! 다중 선형회귀는 단순회귀와 다르게 독립변수가 여러개 있는 것이다.
우선은 간단한 데이터로 감만 먼저 익히고 본격적인 데이터셋으로 완벽하게 이해해보자..
우선 간단한 예제부터 살펴보자. 데이터셋은 임의로 만들어서 사용하였다.
중간고사, 기말고사, 가산점을 독립변수로 두고 최종 점수를 종속변수로 지정하였다.

연습예제

import numpy as np
x = np.array([[70, 85, 11], [71, 89, 18], [50, 80, 20], [99, 20, 10], 
              [50, 10, 10], [20, 99, 10], [40, 50, 20]])    # [중간, 기말, 가산점] 점수
y = np.array([73, 82, 72, 57, 34, 58, 56]) # 최종점수

데이터 생성이 끝났으면 싸이킷런의 LinearRegression 모델을 이용하여 데이터를 fit시킨다. fit()메서드는 LinearRegression모델에 기울기와 절편을 전달하여 계산한다. 여기서는 x가 기울기, y가 절편이 된다.

from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(x, y) 

끝났다.. 이제 최종 점수에 영향을 미치는 중간, 기말, 가산점 점수를 넣고 예측을 진행해보자.
우선 학습한 데이터 x에 대한 예측을 해보고, 훈련때 사용했던 x 말고 다른 데이터도 넣어서 예측해보자.

test1 = model.predict(x)
print(f"기존 데이터를 넣었을 때 결과: {test1}")

test2 = model.predict(np.array([[20,99,10], [90, 90, 20]]))
print(f"새로운 데이터를 넣었을 때 결과: {test2}")

기존 데이터를 넣었을 때 결과: [72.95949786 81.90494749 72.04473132 57.09896022 33.90019234 58.05630987
 56.0353609 ]
새로운 데이터를 넣었을 때 결과: [58.05630987 91.72318972]

결과를 보니 기존 학습에 넣었었던 x 데이터의 결과는 y와 거의 비슷하게 나온것을 확인할 수 있다.
새로운 데이터로 중간20점, 기말99점, 가산점10점을 넣었을 때 최종 점수는 약 58점으로 예측했고, 중간90점, 기말90점, 가산점20점을 넣었을 때는 약 92점을 예측하였다.
참고로 위의 모델은 케라스를 이용해서도 구할 수 있다.
단순 선형회귀때와는 다르게 input_dim에 3을 입력하고 진행하면 된다. 3을 넣는 이유는 x의 데이터shape이 (7, 3)이기 때문이다.

실전예제

이번에는 본격적으로 “분석” 이라는 것을 실시해보자.
지금 실시할 예제는 ‘맨해튼의 주택임대료’ 데이터를 사용한다. 데이터는 여기에서 받을 수 있다.
우선 pandas를 사용하여 데이터를 불러와보자.

import pandas as pd
df = pd.read_csv('manhattan.csv')
df.head()

	rental_id	rent	bedrooms	bathrooms	size_sqft	min_to_subway	floor	building_age_yrs	no_fee	has_roofdeck	has_washer_dryer	has_doorman	has_elevator	has_dishwasher	has_patio	has_gym	neighborhood	borough
0	1545	2550	0.0	1	480	9	2.0	17	1	1	0	0	1	1	0	1	Upper East Side	Manhattan
1	2472	11500	2.0	2	2000	4	1.0	96	0	0	0	0	0	0	0	0	Greenwich Village	Manhattan
2	2919	4500	1.0	1	916	2	51.0	29	0	1	0	1	1	1	0	0	Midtown	Manhattan
3	2790	4795	1.0	1	975	3	8.0	31	0	0	0	1	1	1	0	1	Greenwich Village	Manhattan
4	3946	17500	2.0	2	4800	3	4.0	136	0	0	0	1	1	1	0	1	Soho	Manhattan

우선 데이터의 column을 살펴보자.
id부터 시작해서 침실수, 화장실 수, 면적, 층수 등등 총 18개의 column이 존재한다. 여기서 한번 생각해보자.
무엇이 독립변수이고 무엇이 종속변수일까?
회귀분석을 하려면 어떤 요인이 영향을 미치는지 무엇이 필요없는지 생각부터 해보아야 한다.
지금 이 데이터에서는 ‘rental_id’, ‘neighborhood’, ‘borough’ column이 굳이 종속변수를 예측하는데에 필요가 없어보이지 않는가?
그렇다면 지금 데이터를 수정해보도록 하자. 참고로 종속변수는 ‘rent’ column이다.

# x는 독립변수, y는 종속변수
x = df.drop(['rental_id', 'rent', 'neighborhood', 'borough'], axis=1)
y = df['rent']

이제 데이터를 train과 test로 분리해보자.
분리하는 이유는 나중에 모델의 정확도를 알아보기 위함이다.
모델의 정확도는 train과 test의 잔차(오차)를 계산하여 구한다.
train으로는 오롯이 모델의 학습에만 관여하고, test는 오롯이 모델의 정확도 확인을 위한 데이터로 사용된다.

from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x, y, train_size=0.8, test_size=0.2)

데이터 세트의 분리는 sklearn 제공하는 train_test_split을 통해 손쉽게 할 수 있다. train 데이터는 80%, test 데이터는 20%로 사용하였다.
이제 모델을 생성하자. 방법은 단순선형회귀와 같다. 다만 train 데이터를 가지고 fit시켜야 한다.

from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(x_train, y_train) 

모델을 만들었으면 예측을 해보자!
일단 입력으로는 내가 임의로 값을 넣어보겠다. 독립변수에 대한 값을 넣어주면 된다.

my_apt = [[3, 2, 800, 16, 1, 98, 1, 0, 1, 0, 0, 1, 1, 0]]
print(model.predict(my_apt))

[3992.85165555]

값을 넣었을 때 임대가격은 약 3993달러로 예측했다.
이제 아까 만든 test 데이터로 예측을 해보자.
test 데이터셋의 shape은 (708, 14)이므로 결과적으로 708개에 대한 독립변수 14개를 넣고 예측을 모두 수행한 것이다.

y_pred = model.predict(x_test)
print(y_pred.shape)

(708,)

이제는 회귀계수와 절편을 확인해보자.
다중회귀에서는 기울기의 변수가 많기 때문에 회귀계수라고 부른다.

print(model.coef_)
print(model.intercept_)

[-297.8879704  1208.45292036    4.84749522  -15.28914009   22.07454514
   -7.5426493  -110.82492576  -74.75208813  172.3638424  -190.61610451
  180.78516657   32.42820018 -108.86876524   11.6347591 ]
-431.75347475394483

독립변수가 14개이기 때문에 회귀 계수도 14개가 나왔다. 각 colum별 임대 가격을 선형 회귀선으로 시각화 해보자.

import matplotlib.pyplot as plt
import seaborn as sns
plt.figure(figsize=(20, 10))
plt.rc('xtick', labelsize=6)
plt.rc('ytick', labelsize=6)
for idx, col in enumerate(x):
    ax1 = plt.subplot(2, 7, idx+1)
    sns.regplot(df[col], df['rent'])
    plt.title(f"{col}")

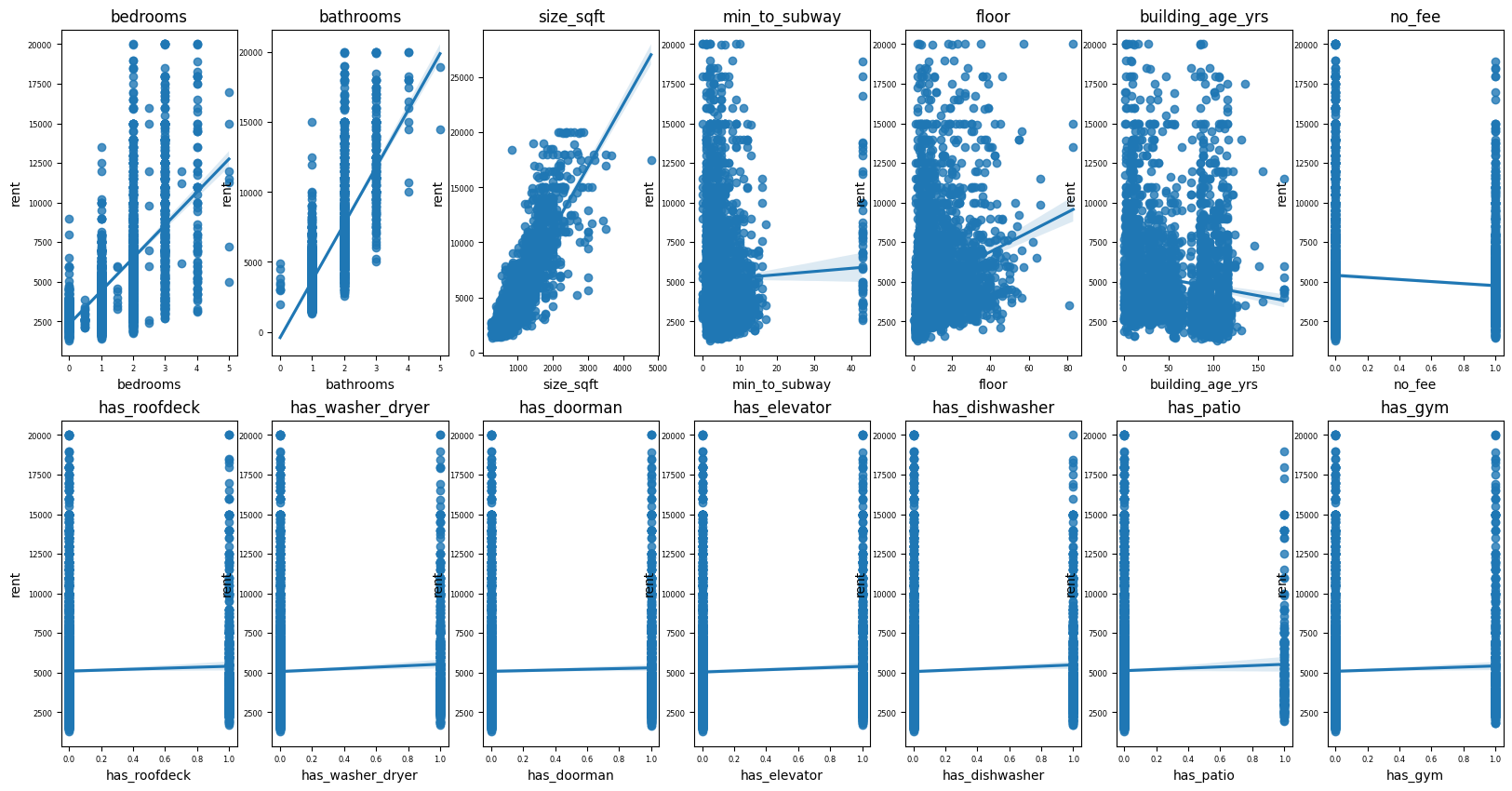
다른 독립변수는 모르겠고, 집의 면적이 임대값에 가장 크게 영향을 미치는 것을 확인할 수 있다.

이제 모델의 정확도를 평가해보자.
모델의 정확도를 평가할 때는 잔차 분석을 하는데, 잔차는 실제 값인 y와 예측한 값인 y_pred의 차이를 말한다.
LinearRegression모델을 사용하여 모델을 생성하면 .score()메서드를 사용할 수 있는데 이 메서드에 y와 y_pred를 넣어주면 결정계수를 반환해준다.
결정계수란 종속변수의 분산 중에서 독립변수로 설명되는 비율을 의미하는데, 쉽게 말해서 이 모델로 대상을 얼마나 잘 설명할 수 있는지를 비율로 나타낸 것이다.
결정계수가 높을 수록 정확도가 높다는 의미이다.

print(model.score(x_train, y_train))

0.7795874502628778

모델의 정확도는 약 78%가 나오는 것을 알 수있다.
꽤 준수한 모델이라고 할 수 있고, 이 의미는 14개의 독립변수로 임대가격의 78%를 설명할 수 있다는 말이다.

마지막으로 각 column별 예측 결과를 시각화 해보자.
파란점이 y이고 빨간점이 y_pred이다.

import matplotlib.pyplot as plt
plt.figure(figsize=(20, 10))
plt.rc('xtick', labelsize=6)
plt.rc('ytick', labelsize=6)
for idx, col in enumerate(x):
    ax1 = plt.subplot(2, 7, idx+1)
    plt.scatter(x_test[col], y_test, s=10)
    plt.scatter(x_test[col], y_pred, c='r', s=10)
    plt.title(f"{col}")

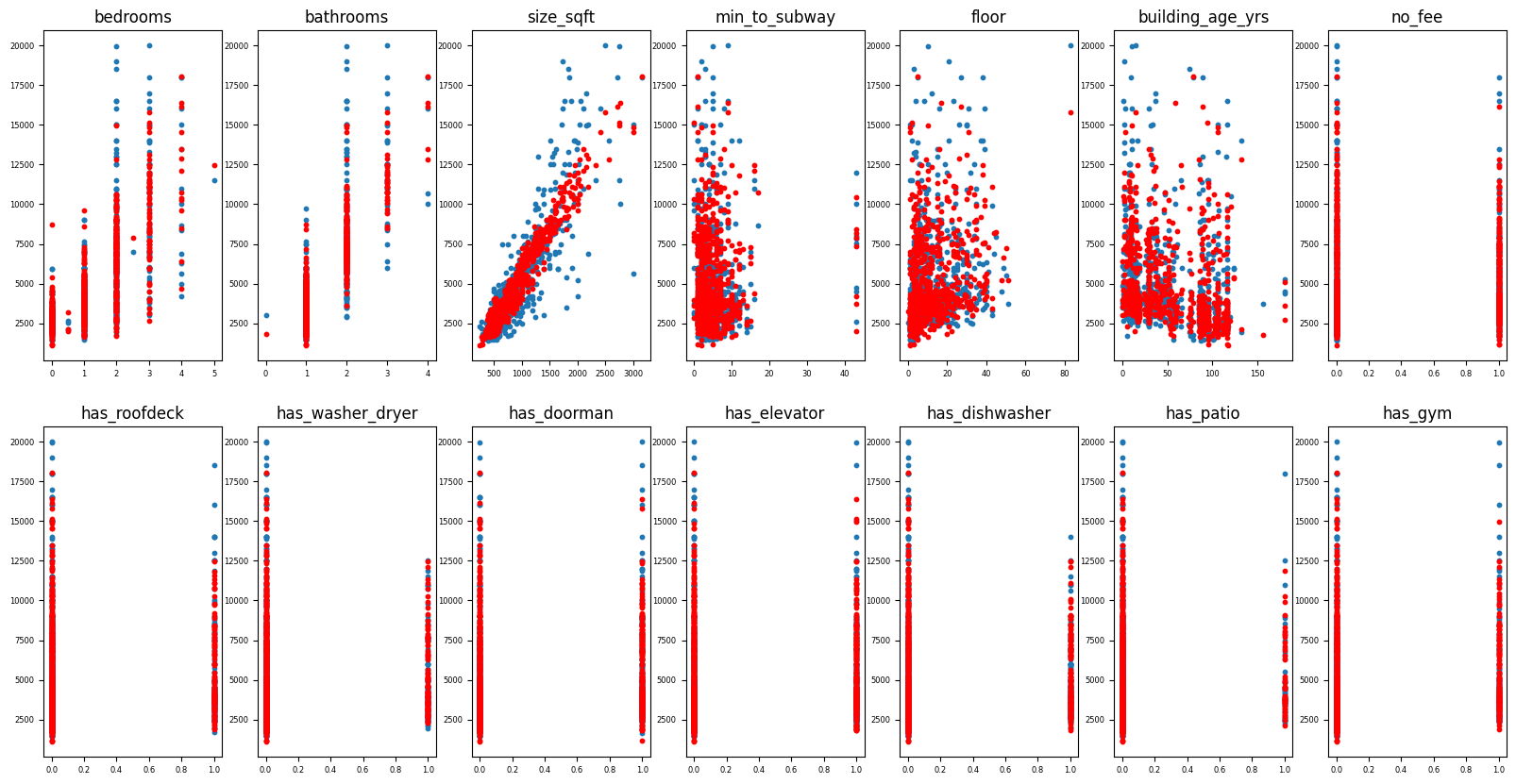
이것으로 오늘의 다중선형회귀분석을 마치도록 하겠다.