다중 로지스틱 회귀분석을 해보자!(1편)

이번에는 다중로지스틱 회귀를 해보자.
로지스틱회귀를 모르는 사람은 이글을 참고하자.

데이터셋 로드

타이타닉 데이터 세트이다. 각 컬럼은
승객 ID, 생존여부, 좌석등급, 승객 이름, 성별, 나이, 함께 탑승한 형제 또는 배우자의 수, 함께 탑승한 부모 또는 자녀의 수, 티켓번호, 티켓요금, 선실번호, 승선위치
를 나타낸다.

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split

data = pd.read_csv("https://raw.githubusercontent.com/datasciencedojo/datasets/master/titanic.csv")
data

	PassengerId	Survived	Pclass	Name	Sex	Age	SibSp	Parch	Ticket	Fare	Cabin	Embarked
0	1	0	3	Braund, Mr. Owen Harris	male	22.0	1	0	A/5 21171	7.2500	NaN	S
1	2	1	1	Cumings, Mrs. John Bradley (Florence Briggs Th...	female	38.0	1	0	PC 17599	71.2833	C85	C
2	3	1	3	Heikkinen, Miss. Laina	female	26.0	0	0	STON/O2. 3101282	7.9250	NaN	S
3	4	1	1	Futrelle, Mrs. Jacques Heath (Lily May Peel)	female	35.0	1	0	113803	53.1000	C123	S
4	5	0	3	Allen, Mr. William Henry	male	35.0	0	0	373450	8.0500	NaN	S
...	...	...	...	...	...	...	...	...	...	...	...	...
886	887	0	2	Montvila, Rev. Juozas	male	27.0	0	0	211536	13.0000	NaN	S
887	888	1	1	Graham, Miss. Margaret Edith	female	19.0	0	0	112053	30.0000	B42	S
888	889	0	3	Johnston, Miss. Catherine Helen "Carrie"	female	NaN	1	2	W./C. 6607	23.4500	NaN	S
889	890	1	1	Behr, Mr. Karl Howell	male	26.0	0	0	111369	30.0000	C148	C
890	891	0	3	Dooley, Mr. Patrick	male	32.0	0	0	370376	7.7500	NaN	Q

891 rows × 12 columns

데이터 전처리

• 불필요한 컬럼 삭제

# 회귀분석에 필요없는 column은 삭제함
data = data.drop(["Name", "Ticket", "Cabin", "PassengerId", "SibSp", "Parch"], axis=1)
data

	Survived	Pclass	Sex	Age	Fare	Embarked
0	0	3	male	22.0	7.2500	S
1	1	1	female	38.0	71.2833	C
2	1	3	female	26.0	7.9250	S
3	1	1	female	35.0	53.1000	S
4	0	3	male	35.0	8.0500	S
...	...	...	...	...	...	...
886	0	2	male	27.0	13.0000	S
887	1	1	female	19.0	30.0000	S
888	0	3	female	NaN	23.4500	S
889	1	1	male	26.0	30.0000	C
890	0	3	male	32.0	7.7500	Q

891 rows × 6 columns

• 비어있는(NaN)값 대체

# 각 columns에 비어있는(NaN)값의 개수 확인
for i in data.columns:
    print(f"{i}: {data[i].isnull().sum().sum()}")

Survived: 0
Pclass: 0
Sex: 0
Age: 177
Fare: 0
Embarked: 2

# 'Age' column의 비어있는 값을 평균값으로 대체
data["Age"].fillna(data["Age"].mean(), inplace=True)

# 'Embarked' column의 비어있는 값을 최빈값('S')로 대체
data["Embarked"].fillna(data["Embarked"].mode()[0], inplace=True)

• 가변수 만들기
  pd.get_dummies을 사용하면 범주형 변수를 숫자형태로 만들 수 있다. 만들어진 결과를 보면 쉽게 이해가 갈것이다.

# "Sex", "Embarked", "Pclass" 칼럼에 가변수를 만들어 준다. 
data = pd.get_dummies(data, columns=["Sex", "Embarked", "Pclass"])
data

	Survived	Age	Fare	Sex_female	Sex_male	Embarked_C	Embarked_Q	Embarked_S	Pclass_1	Pclass_2	Pclass_3
0	0	22.000000	7.2500	0	1	0	0	1	0	0	1
1	1	38.000000	71.2833	1	0	1	0	0	1	0	0
2	1	26.000000	7.9250	1	0	0	0	1	0	0	1
3	1	35.000000	53.1000	1	0	0	0	1	1	0	0
4	0	35.000000	8.0500	0	1	0	0	1	0	0	1
...	...	...	...	...	...	...	...	...	...	...	...
886	0	27.000000	13.0000	0	1	0	0	1	0	1	0
887	1	19.000000	30.0000	1	0	0	0	1	1	0	0
888	0	29.699118	23.4500	1	0	0	0	1	0	0	1
889	1	26.000000	30.0000	0	1	1	0	0	1	0	0
890	0	32.000000	7.7500	0	1	0	1	0	0	0	1

891 rows × 11 columns

데이터 생성

X = data.drop("Survived", axis=1)
y = data["Survived"]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
print(f"총 데이터: {data.shape}\n훈련 데이터: {X_train.shape}\n테스트 데이터: {X_test.shape}\n훈련 라벨: {y_train.shape}\n테스트 라벨: {y_test.shape}")

총 데이터: (891, 11)
훈련 데이터: (712, 10)
테스트 데이터: (179, 10)
훈련 라벨: (712,)
테스트 라벨: (179,)

훈련

# Train the logistic regression model
model = LogisticRegression()
model.fit(X_train, y_train)

print(model.coef_)

[[-3.32869206e-02  9.11449112e-04  1.57447493e+00 -1.09187659e+00
   3.56125647e-01  3.00472417e-01 -1.73999723e-01  1.18739793e+00
   2.62072113e-01 -9.66871700e-01]]

계수는 해당 피처의 변화에 대한 종속변수의 확률 변화를 나타낸다.
로그 확률은 생존(1)과 사망(0) 확률의 비율을 나타내는 odds ratio를 로그로 변환한 것이다.
결과적으로 계수는 각 피처가 종속 변수의 로그 확률에 얼마나 기여하는지 나타낸다.
양의 계수는 해당 피처가 1로 나오는 것에 관련이 있고, 음의 계수는 0으로 나오는것에 관련이 있다.
밑에 그래프를 보자.

importance = model.coef_[0]
feature_importance = pd.DataFrame({"feature": X_train.columns, "importance": importance})
feature_importance.sort_values("importance", ascending=False, inplace=True)
sns.barplot(x=feature_importance["importance"], y=feature_importance["feature"])
plt.show()

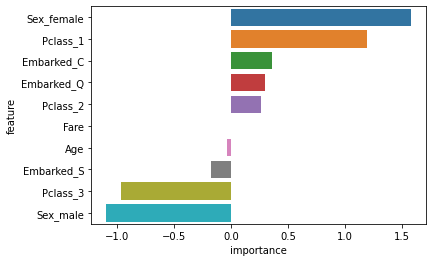
쉽게 말해서, 위의 5개의 독립변수는 생존할 가능성이 높고, 밑에 4개는 생존확률이 낮다는 것을 의미한다.

검증

테스트 데이터셋에 대한 정확도는 약 75%가 나왔다.

model.score(X_test, y_test)

0.7486033519553073

예측

# 나이, 요금, 여자, 남자, 출발지C, 출발지Q, 출발지S, 1등석, 2등석, 3등석
p1 = [[23, 146.5, 1, 0, 1, 0, 0, 1, 0, 0]]
p2 = [[23, 146.5, 0, 1, 1, 0, 0, 0, 1, 0]]
print(f"생존여부: {model.predict(p1)}, 생존확률: {model.predict_proba(p1)}")
print(f"생존여부: {model.predict(p2)}, 생존확률: {model.predict_proba(p2)}")

생존여부: [1], 생존확률: [[0.03859405 0.96140595]]
생존여부: [0], 생존확률: [[0.59299938 0.40700062]]

p1, p2의 나이와 요금, 출발지는 고정했고, p1은 여자, 1등석이고, p2는 남자, 2등석이다.
p1의 생존확률은 약96%이고, p2의 생존확률은 약 40%이다.