단순 선형회귀분석 실습

선형회귀를 모르시는 분들은 선형회귀 한번에 이해하기! 이 글을 참고해 주세요! 데이터는 임의로 만들어서 사용합니다.

방법 1(keras 사용)

우선 필요한 라이브러리를 불러온다.

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras import optimizers
import numpy as np
import matplotlib.pyplot as plt

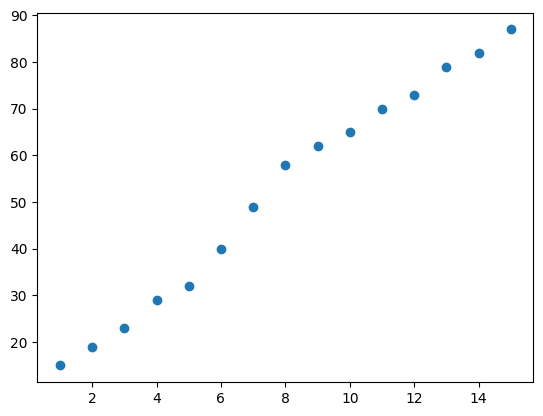
공부시간에 따른 성적변화를 임의로 구성하였다. 데이터 생성후 시각화까지 해보았다.
임의로 데이터를 넣었기 때문에 눈으로 봐도 선형인게 보인다..

x = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]) # 공부 시간
y = np.array([15, 19, 23, 29, 32, 40, 49, 58, 62, 65, 70, 73, 79, 82, 87])  # 성적
plt.plot(x, y, 'o')
plt.show()

모델을 학습하는 단계이다. 앞서 회귀분석 포스트에서 설명한 최적의 기울기와 절편을 구하는 과정이다. 옵티마이저는 경사하강법을 사용했고, 손실함수는 MSE를 사용하여 300번 학습 시켰다. 중요한 점은 단순 선형 회귀분석이기 때문에 x, y가 1차원이다. 만약 다중 선형 회귀라면 input_dim에 2차원으로 들어갔을 것이다.

model = Sequential()

# 출력 y의 차원은 1. 입력 x의 차원(input_dim)은 1
# 선형 회귀이므로 activation은 'linear'
model.add(Dense(1, input_dim=1, activation='linear'))

# sgd는 경사 하강법을 의미. 학습률(learning rate)은 0.01.
sgd = optimizers.SGD(learning_rate=0.01)

# 손실 함수(Loss function)은 평균제곱오차 mse를 사용.
model.compile(optimizer=sgd, loss='mse', metrics=['mse'])

# 주어진 x와 y데이터에 대해서 오차를 최소화하는 작업(학습)을 300번 시도.
model.fit(x, y, epochs=300)

Epoch 1/300
1/1 [==============================] - 0s 155ms/step - loss: 3065.9602 - mse: 3065.9602
Epoch 2/300
1/1 [==============================] - 0s 3ms/step - loss: 1384.0963 - mse: 1384.0963
Epoch 3/300
1/1 [==============================] - 0s 3ms/step - loss: 631.6002 - mse: 631.6002
Epoch 4/300
1/1 [==============================] - 0s 3ms/step - loss: 294.8786 - mse: 294.8786
Epoch 5/300
1/1 [==============================] - 0s 3ms/step - loss: 144.1638 - mse: 144.1638
Epoch 6/300
1/1 [==============================] - 0s 3ms/step - loss: 76.6642 - mse: 76.6642
...
Epoch 39/300
1/1 [==============================] - 0s 3ms/step - loss: 18.2910 - mse: 18.2910
Epoch 40/300
1/1 [==============================] - 0s 2ms/step - loss: 18.1915 - mse: 18.1915
Epoch 41/300
1/1 [==============================] - 0s 2ms/step - loss: 18.0929 - mse: 18.0929
Epoch 42/300
1/1 [==============================] - 0s 3ms/step - loss: 17.9951 - mse: 17.9951
Epoch 43/300
1/1 [==============================] - 0s 2ms/step - loss: 17.8982 - mse: 17.8982
...
Epoch 297/300
1/1 [==============================] - 0s 3ms/step - loss: 8.2467 - mse: 8.2467
Epoch 298/300
1/1 [==============================] - 0s 3ms/step - loss: 8.2369 - mse: 8.2369
Epoch 299/300
1/1 [==============================] - 0s 3ms/step - loss: 8.2271 - mse: 8.2271
Epoch 300/300
1/1 [==============================] - 0s 3ms/step - loss: 8.2175 - mse: 8.2175


<keras.callbacks.History at 0x7f414479f730>

학습된 모델에 x를 넣었을 때 y를 예측하는 단계이다. 여기서는 15.5시간을 넣었을 때 약 94점이 나오는 것을 확인할 수 있다.

print(model.predict([15.5]))

[[93.8742]]

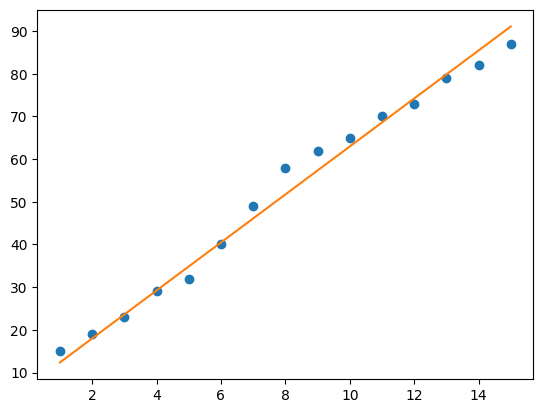
예측한 결과를 바탕으로 선을 그어 보았다. 이 직선이 모델이 예측한 최선의 결과이다. 조금 더 정교한 모델을 만든다면 더 정확한 직선을 그릴것이다.

plt.plot(x, y, 'o')
plt.plot(x, model.predict(x))
plt.show()

방법2(sklearn 사용)

머신러닝 라이브러리인 싸이킷런을 사용하면 더 쉽게 회귀분석을 할 수 있다. 정해진 모델에 데이터만 피팅 시키면 기울기와 절편도 확인이 가능하다. 우선 데이터를 생성하자. 방법1의 데이터와 같게 만들었다.

from sklearn.linear_model import LinearRegression
x = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]) # 공부 시간
y = np.array([15, 19, 23, 29, 32, 40, 49, 58, 62, 65, 70, 73, 79, 82, 87])  # 성적

LinearRegression 모델을 생성하고 데이터를 fit 시키면 끝이다. x에 2차원으로 넣는 이유는 다중회귀분석을 할 때에도 LinearRegression 모델을 쓰기 때문이다.

line_fitter = LinearRegression()
line_fitter.fit(x.reshape(-1,1), y)

정말 간단하다…모델에 predict()메서드를 사용하여 결과를 예측한다. 이 모델에서는 15.5시간을 공부하면 약 73점을 맞는다고 예측했다. 위에 방법과 결과값이 미세하게 다르다.

line_fitter.predict([[15.5]])

array([92.78035714])

사이킷런의 회귀모델을 사용하면 기울기와 절편도 알 수 있다.

print(f"기울기: {line_fitter.coef_}")
print(f"절편: {line_fitter.intercept_}")

기울기: [5.41071429]
절편: 8.91428571428574

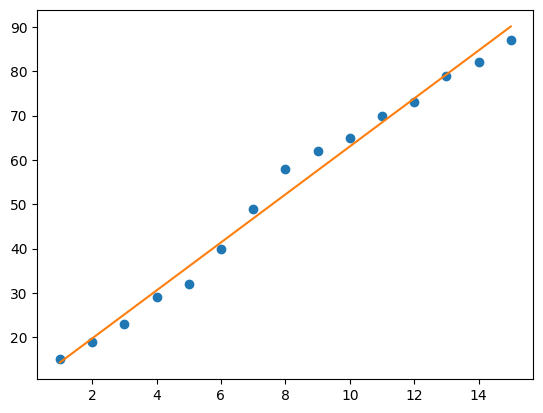
마찬가지로 예측 결과를 바탕으로 선을 그려보았다.

plt.plot(x, y, 'o')
plt.plot(x,line_fitter.predict(x.reshape(-1,1)))
plt.show()

오늘의 정리

다음에는 다중선형회귀분석을 진행해 보도록 하겠다.