DPR(Dense Passage Retrieval for Open-Domain Question Answering) 논문정리
Introduction
-
Dense representation만을 이용해서 Retrieval을 구현함 1) 기존에는 Sparse representation을 사용해서 retrieval을 수행(TF-IDF, BM25) 2)
Q: Who is the bad guy in lord of the rings?
P: Sala Baker is best known for portraying the villain Sauron in the Lord of the Rings trilogy라는 문장이 있을 때, Sparse embedding은bad guy와villain을 매칭 시키기 어렵지만 dense embedding은 매칭이 가능함. -
두 개의 인코더를 사용하여 기존 ORQA의 단점을 보완하고 효과적으로 학습이 가능하다는 것을 입증함. 1) ORQA에서 처음으로 Dense representation을 사용하여 TF-IDF, BM25 같은 모델의 성능을 능가했지만, 인코더를 Fine-tuning하지 않기 때문에 성능이 최대가 아닐 수 있고, ICT(Inverse Cloze Task; 추가적인 pre-training을 위해 마스킹된 문장이 포함된 부분을 예측하는 Task) 의 계산량이 많이 든다는 단점이있음.
-
본 논문에서는 추가적인 pre-training 없이 오직 QA쌍을 이용해서 비교적 적은 데이터를 사용해서 효과적인 학습 체계를 발전시킴.
Contribution
- 적절한 훈련 셋업을 이용해서 기존의 Question-Passage(Answer)쌍에 대한 Q_encoder, P_encoder를 fine-tuning 하는 것이 BM25를 크게 능가하기에 충분하고 ORQA와 다르게 추가적인 사전학습이 필요하지 않음을 보여줌
- 높은 Retrieval 정확도는 높은 end-to-end QA모델의 정확도로 해석할 수 있음을 증명함
DPR
- 모든 question과 passage 쌍을 하나의 배치에서 비교하는 목적함수를 이용해, question vector와 연관있는 passage vector의 내적을
최대화 하여 embedding을 최적화한다.
$sim(q,p)=E_Q(q)^TE_P(p)$
여기서 $E_Q(q)$ 는 Question Encoder를 통과한 question 문장의 벡터이고 $E_P(p)$ 는 Passage Encoder를 통과한 passage 문장의 벡터이다. q와 p는 각각의 인코더에 의해 동일한 dense vector space으로 변환되어 단순히 내적해서 유사도를 계산한다. - 인코더는 어떠한 신경망으로도 구현할 수 있지만 본 논문에서는 2개의 독립적인 BERT 모델을 사용하였다.
- 추론 때에는 모든 Passage에 대해서 $E_P$을 적용하고 FAISS를 사용해서 색인을 생성한다. 런타임 때 질문 q가 주어지면, $E_q$를 적용하여 임베딩을 도출하고 가장 가까운 임베딩을 가진 상위 k개의 passage를 검색한다.
손실함수
- 유사도를 계산할 때 Dot product와 NLL(Nagative Log Likelihood)에 더불어, L2와 triplet loss에 대해서 실험을 진행하였지만,
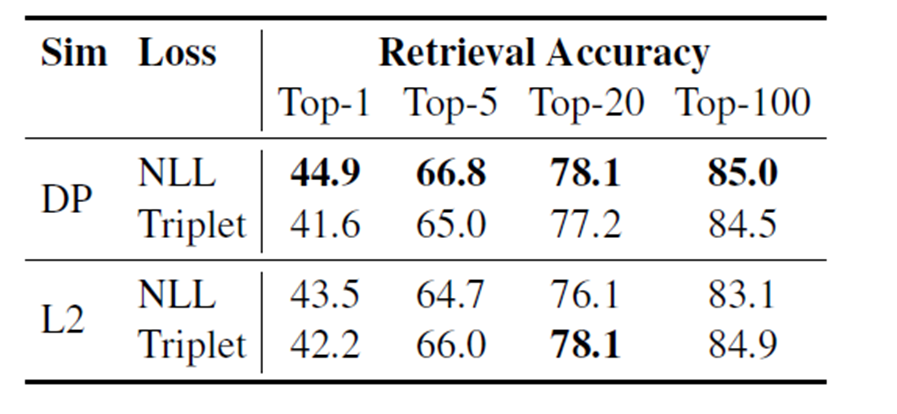
위와 같은 이유로 Dot product와 NLL을 사용함. - 사용한 데이터셋에는 question 1개와 1개의 positive passage, n개의 nagative passage로 구성됨. 실제 데이터셋을 이렇게 구성한 것이 아니고 이런 형식으로 학습에 사용되는데, 자세한 내용은 아래에서 설명한다.
- 질문과 관련된 positive passage, 관련없는 nagative passage 사이의 유사도를 학습함. 아래 수식과 같다.
$L(q_i,p_i^+,p_{i,1}^-,…,p_{i,n}^-)=-log \frac{e^{sim(q_i,p_i^+)}}{e^{sim(q_i,p_i^+)} + \sum_{j=1}^ne^{sim(q_i,p_{i,j}^-)}}$
NLL이므로 분자가 최대한 커져야 L이 최소화 된다. 수식을 보면 $e^{sim(q_i,p_i^+)}$ 이 분자 부분의 값이 커져야 한다. 즉 유사도가 커야한다.
반대로 분모에 $e^{sim(q_i,p_{i,j}^-)}$ 이 부분은 최대한 작아져야 한다. 즉 유사도가 작아져야 한다.
먼저 분자의 값이 작은 경우로 예를 들어보자. $e^{sim(q_i,p_i^+)}$ 이 부분의 값이 1이고 $e^{sim(q_i,p_{i,j}^-)}$ 이 부분의 값이 1000이라고 해보자. 그럼 계산 결과는 1/1000+1이므로 분수의 값은 약 0.001이다.
반대로 $e^{sim(q_i,p_i^+)}$ 이 부분의 값이 1000이고 $e^{sim(q_i,p_{i,j}^-)}$ 이 부분의 값이 1이라고 해보자. 그럼 계산 결과는 1000/1001 이므로 0.99이다.
이 값들에 -log(0.001)과 -log(0.99)를 해보면 3, 0.0043이 된다. 즉 전자의 $L$ 값이 훨씬 더 크다. 따라서 손실함수는 q와 관련된 $p_i^+$의 유사도가 q와 관련없는 $p_{i,j}^-$들에 비해 더 높아지도록 학습하게 된다.
In-batch negatives
사용한 데이터 셋은 question 1개와 1개의 positive passage, n개의 negative passage들로 구성되어 있었다고 했었다.
$D = {{q_i, p_i^+, p_{i,1}^-, … ,p_{i,n}^-}_{i=1}^n}$
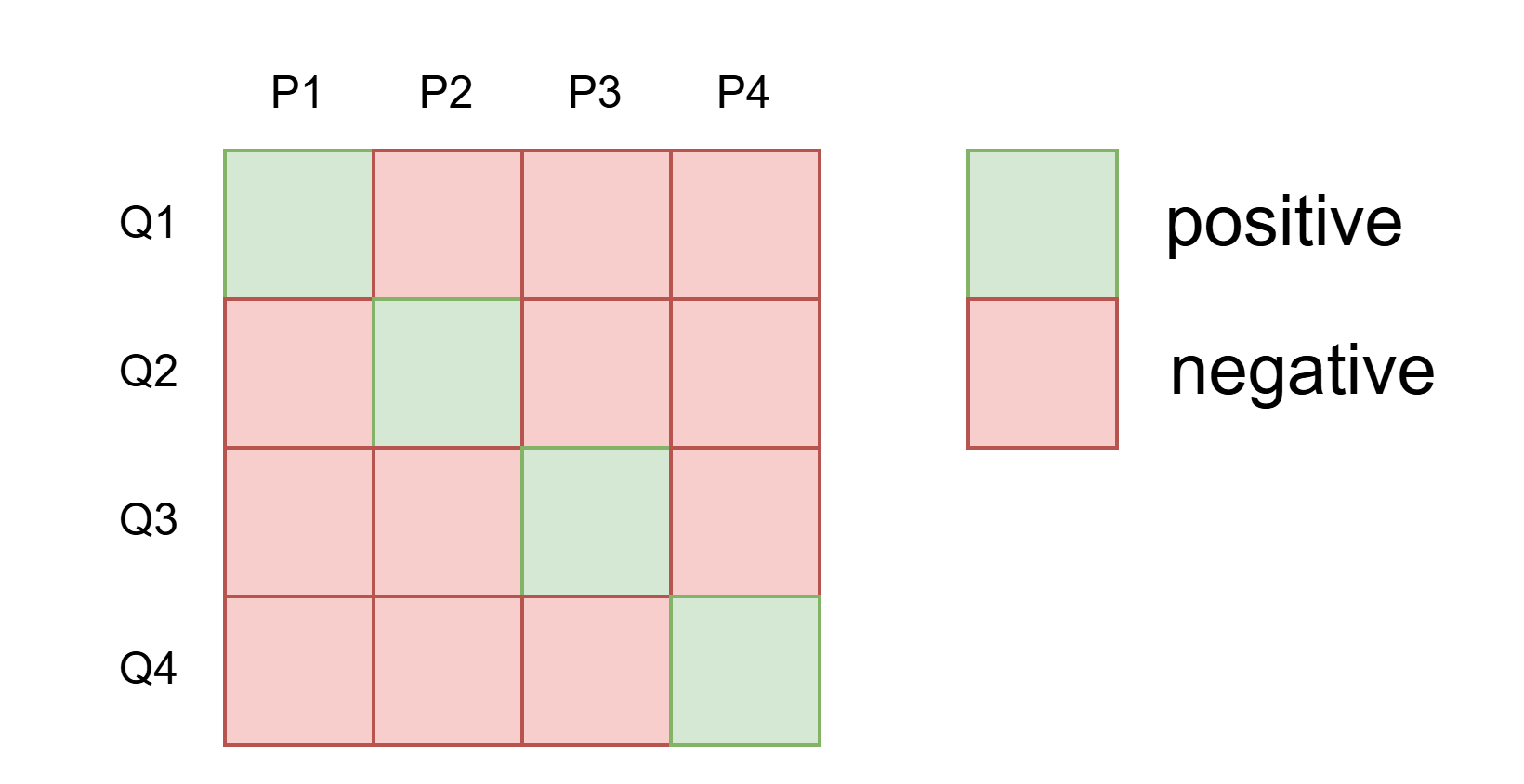
실제 데이터셋을 구성할 때, negative passage는 수집하지 않고 배치 내에서 nagative passage를 사용하는 방식을 고안함.
미니배치 내 N개의 question이 있고, 각 question에는 하나의 positive passage가 있으니까 미니 배치 내에서 자신과 매핑되는 positive passage를 제외한 나머지 positive passage를
nagative passage로 간주하여 학습한다.
Training
batch_size = 128
epoch = 40(NQ, TriviaQA, SQuAD)
epoch = 100(TREC, WQ)
learning_rate = le-5
optimizer = 'adam'
dropout = 0.1
을 사용하였고 BM25기반, DPR 기반, BM25 + DPR 기반을 활용하여 비교 분석을 진행하였다.
BM25 + DPR은 new ranking function을 활용하여 linear combination을 진행하였다. BM25/DPR에서 top-2000개의 passage를 뽑은 후,
다음의 식을 이용하여 top-k 개의 최종 passage를 선택하였다.
$BM25(q,p) + \lambda * sim(q,p)$
결과
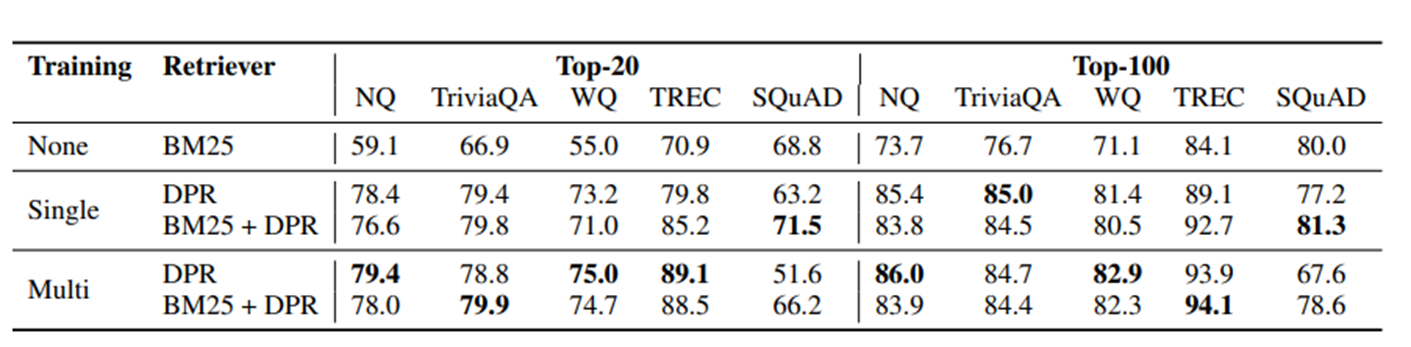

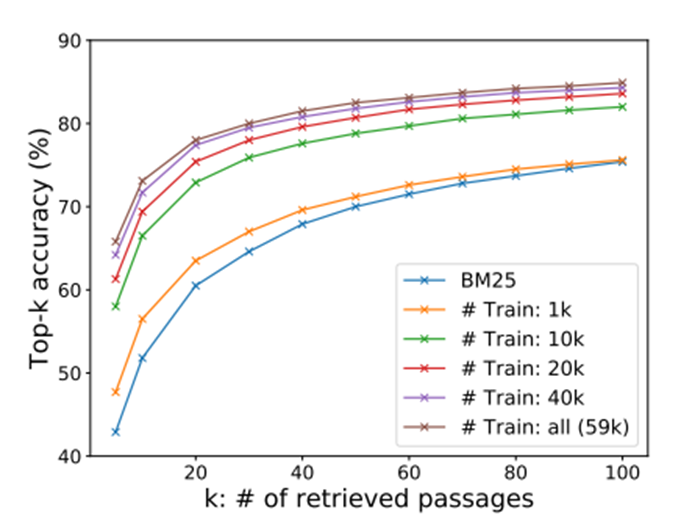
댓글남기기