KAN:Kolmogorov-Arnold Networksv 논문 간단하게 이해하기
본 논문 중 수식적인 부분은 제외하고 최대한 제가 이해한 대로 작성하였습니다. 수식에 관련한 부분은 논문을 참고해 주세요!
Abstract
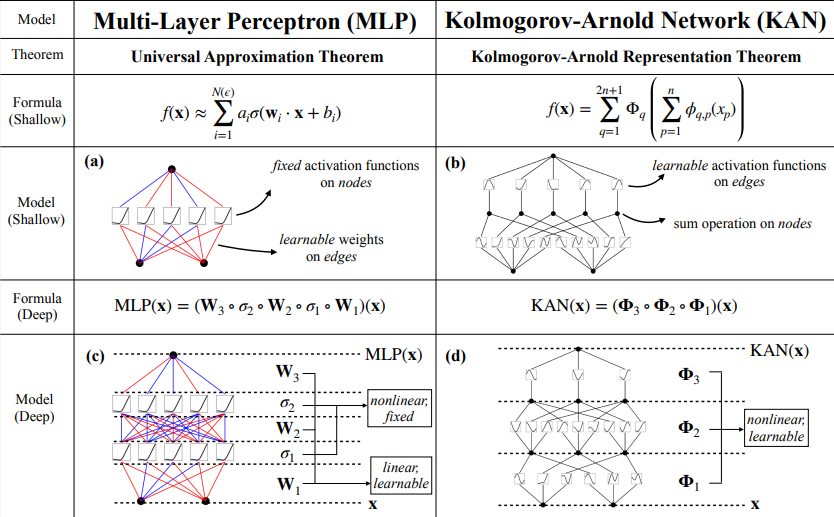
콜모고로프-아놀드 표현 정리에서 영감을 얻어 MLP(다층 퍼셉트론)의 유력한 대안으로 KAN네트워크를 제안한다. MLP는 노드에 활성화 함수가 있는 반면,
KAN은 edge에 ‘학습가능한’ 활성화 함수가 있다. KAN에는 선형 가중치가 전혀 없으며, 모든 가중치 파라미터는 스플라인으로 파라미터화된 단변량 함수로 대체된다.
따라서 정확도와 해석 가능성 측면에서 MLP보다 뛰어나다.
Introduction
MLP의 중요성은 아무리 강조해서 지나치지 않다. 하지만 MLP에는 상당한 단점이 있다. 예를들어, 트랜스포머에서 MLP는 해석 가능성이 높은 특징을 추출하는 도구 없이는 attention layer에 비해 해석 가능성이 떨어진다. MLP와 마찬가지로 KAN도 완전히 연결된 구조를 가지고 있다. KAN에는 선형 가중치 행렬이 전혀 없는 대신 각 가중치 파라미터가 스플라인으로 파라미터화된 학습가능한 1D로 대체된다. KAN은 일반적으로 MLP보다 약 100배 더 작은 계산 그래프를 가진다. 콜모고로프-아놀드 표현을 임의의 폭과 깊이로 일반화 하여 오늘날의 딥러닝 세계에서 이를 활성화하고 맥락화할 뿐만 아니라 광범위한 실증 실험을 통해 정확성과 해석 가능성으로 인해 AI + 과학의 기반 모델로서 잠재적인 역할을 강조하는 데 기여하고자 한다. 엄청난 수학적 해석에도 불구하고 KAN은 스플라인과 MLP의 조합에 불과하여 함수를 정확하게 학습하려면 모델은 구성 구조(외부 자유도)를 학습해야 할 뿐만 아니라 단변량 함수(내부 자유도)도 잘 근사화 해야한다. 결과적으로 KAN은 MLP와의 외부 유사성 덕분에 특징을 학습할 수 있을 뿐 아니라, 스플라인과의 내부 유사성 덕분에 학습한 특징을 매우 정확하게 최적화 할 수 있다. 본 논문에서는 광범위한 수치 실험을 통해 KAN이 MLP보다 정확도와 해석성을 현저히 향상시킬 수 있음을 보여준다.
KAN architecture
입출력 쌍 $x_i$, $y_i$로 구성된 작업이 있고, 모든 데이터 포인트에 대해
$y_i\approx f(x_i)$ 가 되도록 f를 찾고자 한다고 가정할 때,
학습할 모든 함수는 단변량 함수이므로 각 1D 함수를 B-spline curve로 매개변수화 할 수 있으며,
로컬 B-spline 기반함수의 학습가능한 계수를 사용할 수 있다.(아래 그림 오른쪽 부분)
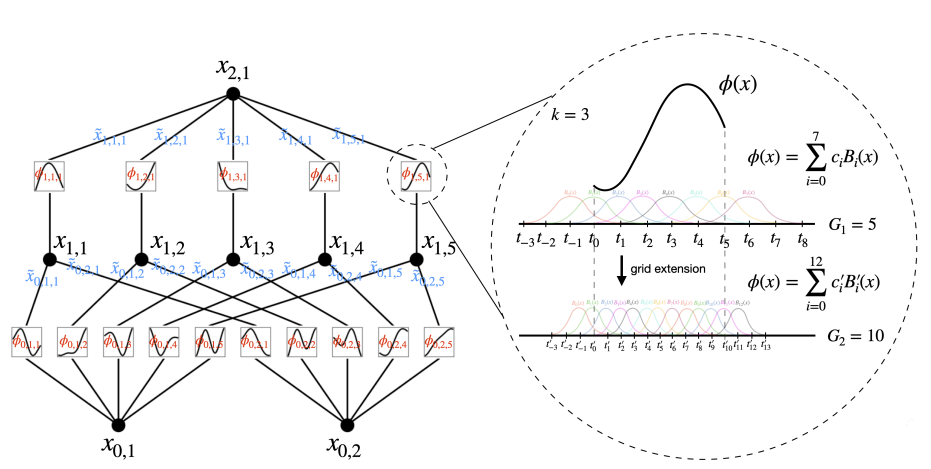
$f(x) = f(x_1, \cdots, x_n) = \sum_{q=1}^{2n+1} \Phi_q\left(\sum_{p=1}^n \phi_{q,p}(x_p)\right)$
콜모고로프-아놀드 표현 정리에 따라 Abstract의 그림처럼 입력 차원이 2이고,
활성화 함수가 노드 대신 edge에 배치되고 중간층에 2n+1의 2계층 신경망으로 나타낼 수 있다.
본 논문에서는 KAN Layer를 계속 쌓는 방법으로 수식을 변환시켰다.
$\text{KAN}(x) = (\Phi_{L-1} \circ \Phi_{L-2} \circ \cdots \circ \Phi_1 \circ \Phi_0)(x)$
이제 모든 연산이 미분 가능하므로 역전파를 통해 KAN을 훈련할 수 있다.
MLP는 선형 변환과 비선형성을 W와 \sigma로 개별적으로 처리하는 반면, KAN은 \Phi로 모두 함께 처리한다.
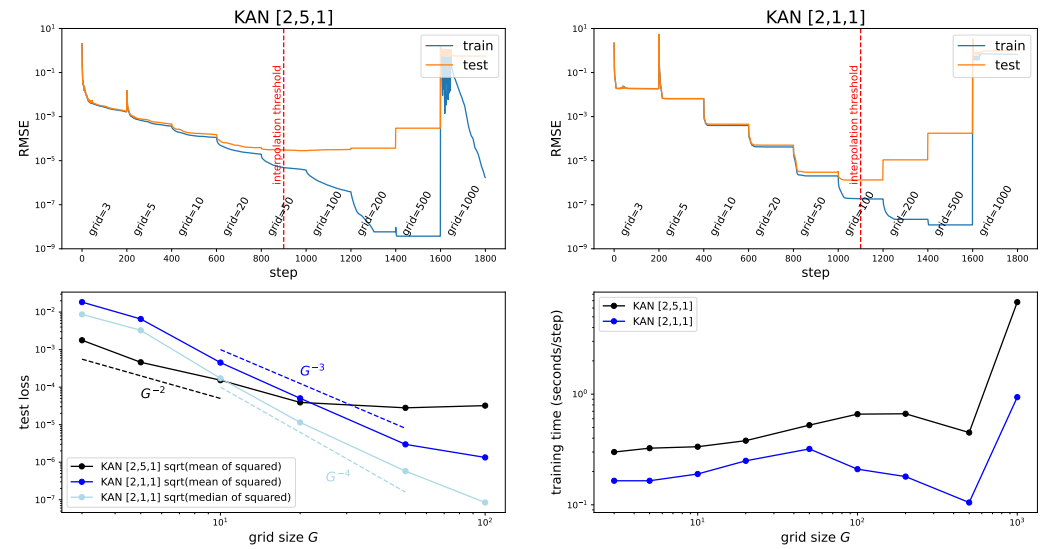
본 논문은 grid extension 기법을 통해 KAN을 더 정확하게 만든다. 위 사진의 맨 윗부분 두개는 grid extension 후 손실이 감소되는 것을 나타낸다.
또한 grid extension 크기에 따라 훈련 시간도 유리하게 작용하는 것을 알 수 있다.
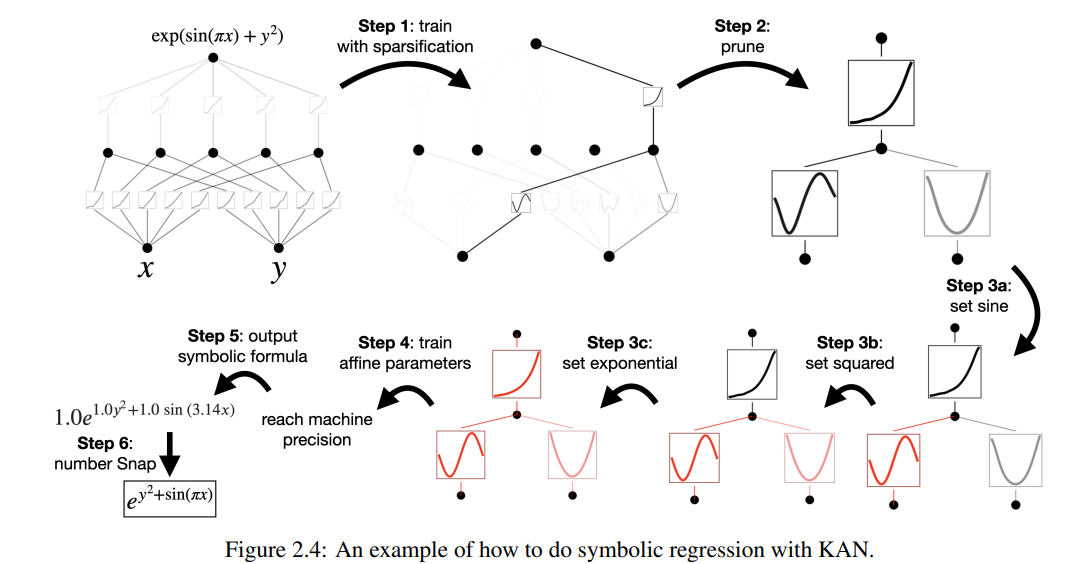
위 사진은 KAN을 사용하여 회귀를 수행하는 방법을 나타낸 것이다.
KAN’s Accurate
KAN은 다양한 작업에서 MLP보다 기능을 표현하는데 더 효과적이다. 두 가지 모델을 비교했을 때, KAN이 MLP보다 정확도와 복잡성 측면에서 더 유리하다는 것을 입증했다.
또한 KAN은 파괴적 망각 없이 Continual learning을 수행할 수 있다는 것을 보여준다.
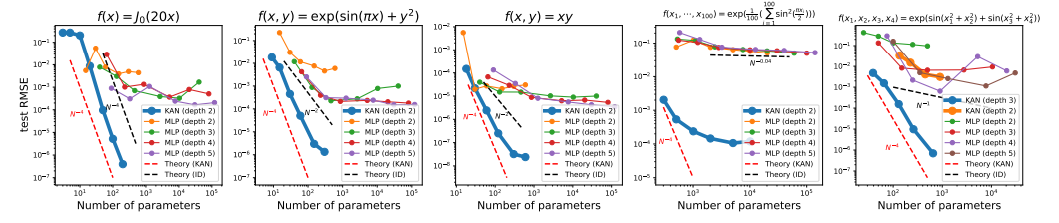
위 그림은 토이 데이터셋을 통해 KAN와 MLP를 비교한 것이다. KAN은 빠르게 스케일링 되지만 MLP는 천천히 스케일링 된다.
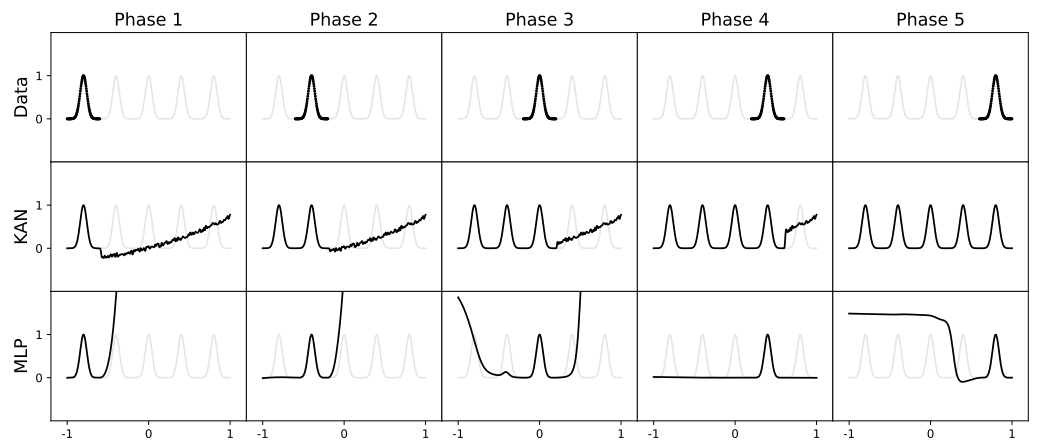
KAN은 스플라인 베이스가 로컬이기 때문에 샘플은 가까운 스플라인 계수 몇 개에만 영향을 미치고 멀리 있는 계수는 그대로 유지하는 원리에 의해 파괴적 망각을 피할 수 있다.
멀리 있는 영역이 보존하려는 정보를 이미 저장했기 때문이다. 위 그림에서 처럼 KAN은 현재 단계에서 데이터가 있는 지역만 리모델링하고 이전 지역은 변경되지 않는다.
하지만, MLP는 새로운 데이터 샘플을 본 후 전체 영역을 리모델링하여 치명적인 망각을 초래한다.
모델의 해석력 측면은 추가로 업데이트 예정
느낀점
기존 MLP말고 새로운 네트워크가 나왔다는 것에 굉장히 흥미로웠다. 정확도와 해석력이 높다지만 Transformer, 비전 관련 아키텍쳐의 적용했을 때의 결과가 논문에는 나와있지 않아서 아직 확신하긴 이른 것 같다. 앞으로의 연구가 굉장히 기대되고 나도 여러가지 실험을 해보고 싶다. 요즘 Continual Learning을 공부중인데 catastrophic forgetting 극복이 가능하다는 것이 정말 인상깊었다. 세상은 넓고 정말 천재들은 많은 것 같다….

댓글남기기