DDPM 논문리뷰
Abstract
우리는 비평형 열역학에서 영감을 얻은 잠재 변수 모델의 클래스인 확산 확률 모델을 사용하여 고품질 이미지 합성 결과를 제시한다. 우리의 결과는 확산 확률 모델과 Langevin 역학의 denoising score 사이의 새로운 연결에 따라 디자인된 variational bound 가중치에 대한 훈련으로 얻어지며, 우리 모델은 자연스럽게 자기회귀 디코딩의 일반화로 해석될 수 있는 점진적 손실 압축 해제 방식을 사용한다. 그 결과 CIFAR10 데이터 세트에서 우리는 9.46의 Inception 점수와 3.17의 최첨단 FID 점수를 얻었다.
Introduction
확산 확률 모델(간단함을 위해 “확산 모델”이라고 함)은 유한한 시간 후에 데이터와 일치하는 샘플을 생성하기 위해 variational inference를 사용하여 훈련된 Markov 체인이다. 이 체인은 신호가 파괴될 때까지 샘플링의 반대 방향으로 데이터에 노이즈를 점진적으로 추가하는 Markov 체인인 diffusion 프로세스를 역전하도록 학습된다. diffusion이 소량의 가우시안 노이즈로 구성된 경우 샘플링 체인 전환을 조건부 가우시안으로 설정하는 것으로 충분하므로 특히 간단한 신경망 매개변수화가 가능하다.
Diffusion Model

diffusion model은 생성 모델로써 학습된 데이터의 패턴을 생성해 내는 역할을 한다. 패턴 생성 과정을 학습하기 위해 고의적으로 패턴을 무너뜨리고, 이를 다시 복원하는 확률밀도함수를 학습한다.
$q(x_t|x_{t-1})$로 부터 조건부가 바뀐 $p(x_{t-1}|x_t)$는 추론과정에서 활용이 불가능하지만 $q(x_t|x_{t-1})$가 가우시안 분포를 따르면 $p(x_{t-1}|x_t)$분포도 가우시안을 따른다. 따라서
$q(x_{t-1}|x_t)$의 분포를 추정하는 $p_\theta(x_{t-1}|x_t)$를 학습하게 된다. noising과 denoising과정을 단일 step에 학습하는 것은 어려우므로 논문에서는 1000번의 step으로 Markov chain을 사용하여 구성한다.
Diffusion Process(data -> noise)
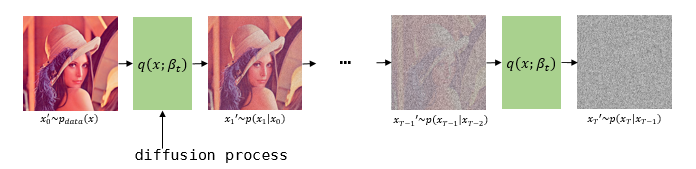
| diffusion process란 사진과 같이 데이터에 노이즈를 추가하는 과정이다. 논문에서 $q$는 diffusion process이며 미세한 가우시안 노이즈를 추가한다. 주어진 데이터를 $x_0$라고 할 때, $x_0$에서 노이즈를 추가하여 $x_1$을 만드는 것을 $q(x_1 | x_0)$라고 표현할 수 있다. 이 식을 time $t$에 대해 표현하면 $q(x_t | x_{t-1})$처럼 표현이 가능하다. 추가로 $q$는 Markov chain이고 $x_t$가 커질수록 그 이전시점은 독립적이다. 결국 $x_T$로 갔을때는 $N(x_T;0,1)$처럼 가우시안 분포를 따르게 된다. 이를 수식으로 표현하면 다음과 같다. |
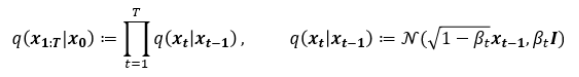
이전 state인 $x_{t-1}$을 조건으로 갖는 조건부분포 $q(x_t|x_{t-1})$는 위와 같이 정의된다.
여기서 $\beta$는 노이즈의 크기이다. data에 noise를 추가할때, 분산 스케쥴링(variance schedule)을 이용하여 scaling한 후 더해준다. 매 step마다 정규분포에서 reparameterization을 통해 sampling하는데, $\sqrt{1-\beta_t}$로 scaling하는 이유는 분산이 발산하는 것을 막기 위함이다. 이 값은 학습가능한 매개변수로 둘 수도 있지만, 실험을 해보니 별 차이가 없어서 본 논문에서는 이 부분을 하이퍼파라미터로 사용한다. 다시말해서, diffusion process과정에서는 학습을 하지 않는다.
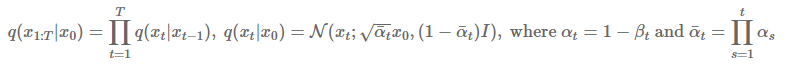
diffusion process의 variance $\beta_t$에 대한 스케쥴을 $\beta_T$까지 설정하고 조건부분포가 정의 된다면, 어떤 데이터 $x_0$에 대한 $x_t$의 분포를 정의할 수 있다. 따라서 $q(x_t|x_0)$에 대한 조건부분포는 위의 수식과 같이 정의된다.
Reverse Process(noise -> data)
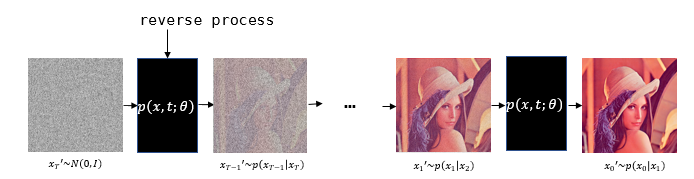
| reverse process는 diffusion process와는 반대로 가우시안 노이즈를 걷어내는 과정이다. 논문에서 $p$는 reverse process이며 미세한 가우시안 노이즈를 걷어낸다. $p$또한 Markov chain이다. 완전히 noise화 된 데이터를 $x_T$라고 할 때, $x_T$에서 노이즈를 추가하여 $x_{T-1}$을 만드는 것을 $p(x_{T-1} | x_T)$라고 표현할 수 있다. 마찬가지로 time $t$에 대해서 표현하면 $p(x_{t-1} | x_t)$로 표현이 가능하다. 이를 수식으로 표현하면 다음과 같다. |
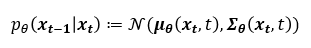
식에서 $\theta$를 포함하도록 하여 학습되는 모델임을 명시하였다. 이 과정은 $\mu$와 $\Sigma$를 파라미터로 갖는 가우시안 분포로 이루어진다. 따라서 우리는 최적의 값을 찾기 위해 학습이 필요한 부분이다.
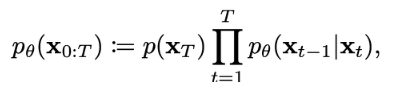
위 수식은 $x_T$부터 $x_{0:T}$까지의 누적합을 나타낸다.
DDPM Loss

| 위의 수식은 VAE와 얼추 비슷하다. ELBO식의 분모가 latent의 KLD loss를 가르는 것이 아니라 VAE에서 Reconstruction term이 되는 분자와 합쳐져서 결국 $p_\theta(x_0 | x_T)$와 $q(x_T | x_0)$의 KLD를 최소화 하는 term이 된다. 그러면 q로부터 어떻게 p를 학습시킬 수 있는지 의문이 든다. 보시다시피 두 분포의 condition이 서로 반대이다. 이를 수식으로 풀어내면 아래와 같다. |

기본적인 것은 수식 옆에 글로 설명해 놓았다. 중요한 부분은 8번째 줄에서 VAE와 같은 트릭으로 같은 값을 곱하는 것과 같은 수식 전개로 수식 내의 $p$와 $q$의 분포가 서로 같은 condition을 나타내게끔 수식을 전개한다. 수식 마지막 부분에는 3개의 loss term이 나오게 된다.
$L_t$ term
여기서는 사후분포가 가우시안 노이즈를 따르도록 강제 하는 loss이다. 논문에서는 실제로 $\beta_1 = 0.0001$부터 $\beta_t = 0.02$까지 linear하게 증가한다고 하고, 이에 따라 $q(x_T|x_0)$을 계산해 보면 $N(x_T;0.00635x_0, 0.99995I)$로 $N(0,1)$인 정규분포와 가까워 진다. 즉 noise latent인 $x_T$를 얻을 때, VAE와 같이 어떤 분포를 따라갈 필요없이 $x_T$의 샘플링은 가우시안 분포에서 이루어진다. 쉽게 말해서 $x_T$가 항상 가우시안 분포를 따르도록 하고 $q(x_T|x_0)$은 $p_\theta(x_T)$와 유사하기 때문에 항상 0에 가까운 상수이며, 학습을 진행할 필요가 없다.
$L_{t-1}$ term
DDPM에서 가장 핵심이 되는 구간이다. 이해하기가 매우 어려웠다… 이 term은 diffusion process의 사후분포를 예측하는 loss이다. $x_0$부터 시작해서 conditional하게 식을 전개하다 보면 tractable한 $q(x_{t-1}|x_t,x_0)$의 정규분포를 알 수 있는데, 이를 바탕으로 KLD를 계산하면 우리가 결과적으로 원하는 $p_\theta(x_{t-1}|x_t)$를 학습시킬 수 있다. 여기서 $q(x_{t-1}|x_t,x_0)$는 다음과 같은 수식으로 정의한다.
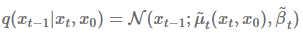

확률밀도함수를 대입하여 $q(x_{t-1}|x_t,x_0)$를 직접 구하지는 않았다. 중요한것은 맨 밑에 $\tilde{\mu}(x_t,x_0)$와 $\tilde{\beta}_t$의 값을 도출 할 수 있다는 것이다.

이제 $L_{t-1}$을 구해보도록 하자. 본 논문에서는 $\tilde{\beta}tI$의 값을 $\sigma_t^2I$로 두었고, 이는 t시점까지의 누적된 noise를 나타낸다. 여기서 중요한 점은 $x_t(x_0,\epsilon)$의 값을 추가로 도출했다는 것이다. 이 값은 reparameterization trick으로 구할 수 있고 이 값을 각각 $L{t-1}$식의 $x_t$에 대입하여 풀어보면 아래와 같은 식이 도출된다. $x_t(x_0,\epsilon)$으로 $\mu_\theta(x_t,t)$식을 다시 정리하는데 이를 Denoising matching이라고 한다. 논문에서는 이러한 새로운 방법을 도출하여 성능을 높였다고 한다. 결국 $\mu_\theta$의 값은 $x_t$가 주어졌을 때, 위 수식의 마지막을 예측하도록 학습하게 된다. 논문에서 최종적으로 도출된 loss는 아래와 같다. 결국 우리가 학습해야 하는 모델은 $\epsilon_\theta$가 된다.
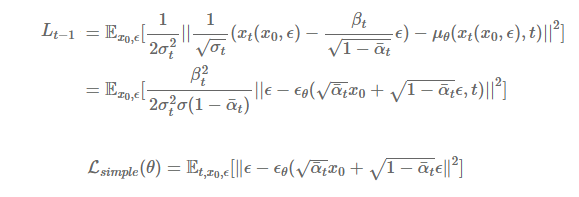
$L_0$ term
이 term은 마지막 latent $x_1$에서 data $x_0$으로의 reconstruction error를 나타낸다. VAE는 $z$~$N(0,1)$에서 image에 대한 reconstrction이었다면, DDPM의 reconstruction은 아주 미세하게 노이즈한 이미지에서 원래의 image로의 reconstruction이므로 모델입장에서는 매우 쉬운 task라고 할수있다. 식으로 나타내면 아래와 같다.
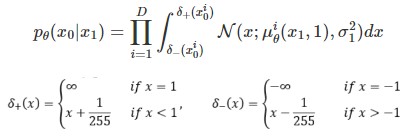
수식으로 보면 어려워 보이지만 이미지 $x_{t=0}$에 대해 $x_{t=1}$을 집어넣어서 나온 결과를 $x_{t=0}$와의 MSE loss를 최소화 하는 것과 같다.
Experiments
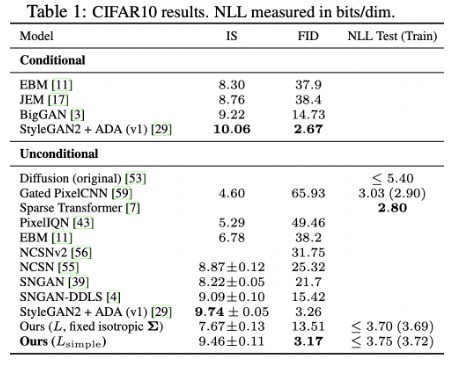
DDPM의 FID score는 3.17로 StyleGAN2+ADA를 이길 만큼의 좋은 모습을 보여주고 있다. 계수 term을 제외한 경우는 제외하지 않은 경우에 비해 NLL이 높은것을 볼 수 있지만, 절반이상이 왜곡 수치이고 이는 감지할 수 없는 작은 값이라고 설명한다.
IS score는 생성된 image로 부터 분류를 할 때, 얼마나 특정 class로 추정을 잘 하는지에 대한 score이고 높을 수록 좋다. FID는 실제 데이터를 참고하여 평균과 공분산을 비교하는 score이며 낮을 수록 좋다.

다음은 Objective function에 관한 내용이다. 결과적으로 $\epsilon$을 예측하는 것이 성능이 더 좋게 나온것을 알 수 있다. 식 3과 4를 보게되면, 식 3은 계수 term이 존재하는데 이는 t가 증가할 수록 그 값이 작아지는 경향을 같게 된다. 따라서 계수가 존재할 경우 더 noisy한 시점의 loss가 상대적으로 down-weight되는 효과가 발생한다고 한다. 식 4는 계수를 제거함으로써 더 noisy한 시점의 loss 비중을 더 높일 수 있고 denoising에 집중하도록 유도하기 때문에 성능이 좋다고 한다.
오늘의 정리
일단 난이도가 극악이고 이해가 안되는 수식이 몇 있다. 제일 중요한 것은 $L_{t-1}$ term인데 분포가 정 반대인 $p$와 $q$를 동일한 condition으로 만들었다는 것이 제일 핵심인 것 같고, $x_{t-1}$에서 noise를 더해 $x_t$까지 만들었을 때, 그 과정을 복원하는 과정을 학습한다는 것이 핵심인것 같다.

댓글남기기