시계열데이터 이진분류
오늘은 시계열 데이터를 이미지로 바꿔서 정상, 비정상 분류를 해보겠다.
부끄럽지만,, 학부생 논문으로 낸 프로젝트이다.(논문은 여기로)
사용한 데이터는 기계시설물 고장 예지 센서 데이터를 사용하였다.
데이터는 여기에서 받을 수 있다.
본 포스팅에서 데이터의 구조는 따로 설명을 안하니, 위 링크로 가서 확인해보길 바란다.
import pandas as pd
import numpy as np
import os
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1 import ImageGrid
from pyts.image import GramianAngularField
from glob import glob
데이터 로드
normal_path = "./L-EF-04/정상/"
abnormal_path = './L-EF-04/회전체불평형/'
#current/2.2kW/L-EF-04/
load_files()함수는 경로 내에 csv 파일을 가져온다.
def load_files(path):
files = []
filelist = sorted(glob(f'{path}/*.csv'))
for file in filelist:
files.append(file)
return files
normal_list = load_files(normal_path)
abnormal_list = load_files(abnormal_path)
print(f"정상파일 개수: {len(normal_list)}\n비정상파일 개수: {len(abnormal_list)}")
정상파일 개수: 667
비정상파일 개수: 229
make_df() 함수는 가져온 csv파일을 데이터프레임으로 변경한다.
csv에 데이터에 대한 설명이 9줄이 있는데, skiprows를 통해서 설명은 제거하고 데이터만 추출하였다.
def make_df(file_list):
li = []
df_list = [pd.read_csv(file,
encoding='utf-8',
header=None,
names=['timestamp', 'R', 'S', 'T', 'NaN'],
skiprows=9) for file in file_list]
for df in df_list:
df.drop('NaN', axis=1, inplace=True)
df.set_index('timestamp', inplace=True)
li.append(df)
return li
normal_df = make_df(normal_list)
abnormal_df = make_df(abnormal_list)
normal_df[0].head()
| R | S | T | |
|---|---|---|---|
| timestamp | |||
| 0.0000 | -0.600586 | -3.203125 | 3.363281 |
| 0.0005 | 0.000000 | -3.563477 | 3.083008 |
| 0.0010 | 0.800781 | -3.803711 | 2.482422 |
| 0.0015 | 1.681641 | -4.083984 | 1.881836 |
| 0.0020 | 2.482422 | -4.164062 | 1.241211 |
데이터 시각화
정상과 비정상이 뭐가 다른지 잘 모르겠지만,, 일단 시각화를 해보았다.
plt.figure(figsize=(18, 5))
plt.subplot(121)
plt.plot(normal_df[200], label=['R','S','T'])
plt.legend()
plt.title("Normal")
plt.subplot(122)
plt.plot(abnormal_df[200], label=['R','S','T'])
plt.legend(loc='lower right')
plt.title("abnormal")
plt.show()
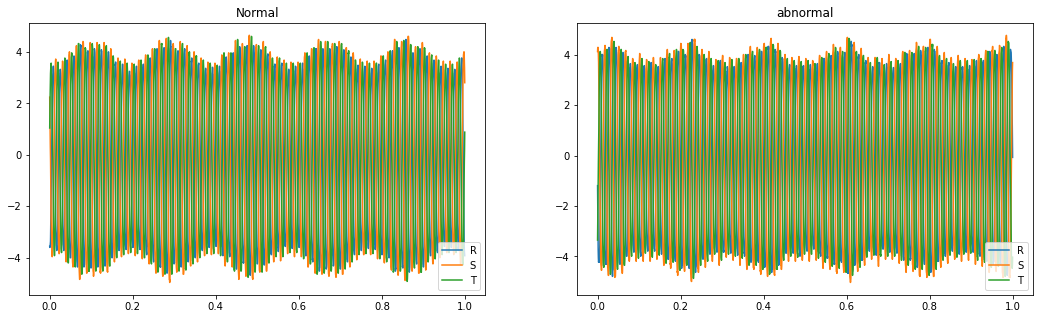
이미지 변환
data_gaf()함수는 pyts에서 제공하는 GAF 방식으로 데이터를 이미지로 변환한다.
원래 csv파일 1개당 시계열 데이터가 2000개가 있는데, timestamp를 2000으로 잡으면 변환시간도 너무 오래걸리고, 이미지도 복잡해지기 때문에 50으로 설정하였다.
중간에 T(Transpose)는 (None, 50, 3)을 (None, 3, 50)으로 바꿔서 timestamp를 피처로 사용하기 위해서 전치를 해주었다.
그러면 (None, 3, 50, 50)으로 바뀌는데 이것을 다시 (None, 50, 50, 3)으로 바꾸기 위해 전치를 해주었다.
def data_gaf(df_list):
li = []
concat_df = pd.concat(df_list).values.reshape(-1, 50, 3)
for i in concat_df:
gaf = GramianAngularField()
X_gaf = gaf.fit_transform(i.T)
li.append(X_gaf.T)
return np.array(li)
normal_X = data_gaf(normal_df)
abnormal_X = data_gaf(abnormal_df)
print(f"정상이미지: {normal_X.shape}\n비정상이미지: {abnormal_X.shape}")
정상이미지: (26680, 50, 50, 3)
비정상이미지: (9160, 50, 50, 3)
데이터 라벨링
data_labeling()함수는 정상을 0, 비정상을 1로 라벨링하고, 데이터와 라벨을 합쳤다.
데이터는 정상, 비정상 데이터로 X가 되고, 라벨은 정상, 비정상 라벨로 y가 되겠다.
def data_labeling(data, normal=True):
if normal == True:
normal_Y = np.zeros((data.shape[0]))
return normal_Y
else:
abnormal_Y = np.ones((data.shape[0]))
return abnormal_Y
normal_Y = data_labeling(normal_X)
abnormal_Y = data_labeling(abnormal_X, normal=False)
print(normal_Y.shape)
print(abnormal_Y.shape)
(26680,)
(9160,)
from sklearn.utils import shuffle
X = np.concatenate((normal_X,abnormal_X))
y = np.concatenate((normal_Y,abnormal_Y))
# X, y = shuffle(X, y)
print(X.shape)
print(y.shape)
(35840, 50, 50, 3)
(35840,)
훈련세트 설정
X, y에서 먼저 train과 test를 설정하고, test데이터에서 20%만큼을 valid데이터로 사용하였다.
valid데이터는 모델 학습시 정확도와 손실값을 보기 위한 용도로만 사용된다.
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.3, shuffle=True, stratify=y, random_state=50)
x_test, x_val, y_test, y_val = train_test_split(x_test, y_test, test_size=0.2, shuffle=True, stratify=y_test, random_state=50)
print(x_train.shape)
print(x_test.shape)
print(x_val.shape)
print(y_train.shape)
print(y_test.shape)
print(y_val.shape)
(25088, 50, 50, 3)
(8601, 50, 50, 3)
(2151, 50, 50, 3)
(25088,)
(8601,)
(2151,)
정규화
x_train = (x_train - np.min(x_train)) / (np.max(x_train)- np.min(x_train))
x_test = (x_test - np.min(x_test)) / (np.max(x_test)- np.min(x_test))
x_val = (x_val - np.min(x_val)) / (np.max(x_val)- np.min(x_val))
print(x_train.shape)
print(x_test.shape)
print(x_val.shape)
(25088, 50, 50, 3)
(8601, 50, 50, 3)
(2151, 50, 50, 3)
모델생성
import tensorflow as tf
plt.style.use('seaborn-white')
from tensorflow.keras import Model
from tensorflow.keras.models import Sequential
from tensorflow.keras.utils import to_categorical
from tensorflow.keras.layers import Dense, Flatten, Conv2D, MaxPool2D, Dropout, Input
from tensorflow.keras.callbacks import EarlyStopping, ModelCheckpoint
model = Sequential()
model.add(Conv2D(32, (3,3), input_shape=(50,50,3), activation='relu', padding='same'))
model.add(Conv2D(64, (3,3), activation='relu', padding='same'))
model.add(MaxPool2D(pool_size=(2,2)))
model.add(Dropout(0.5))
model.add(Flatten())
model.add(Dense(256, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
history = model.fit(x_train, y_train, epochs=20, validation_data=(x_val, y_val), batch_size = 32)
Epoch 1/20
784/784 [==============================] - 63s 80ms/step - loss: 0.3615 - accuracy: 0.8219 - val_loss: 0.2642 - val_accuracy: 0.8698
Epoch 2/20
784/784 [==============================] - 62s 79ms/step - loss: 0.2653 - accuracy: 0.8675 - val_loss: 0.2423 - val_accuracy: 0.8819
Epoch 3/20
784/784 [==============================] - 62s 79ms/step - loss: 0.2349 - accuracy: 0.8867 - val_loss: 0.2541 - val_accuracy: 0.8763
Epoch 4/20
784/784 [==============================] - 62s 79ms/step - loss: 0.2140 - accuracy: 0.8979 - val_loss: 0.1942 - val_accuracy: 0.9145
Epoch 5/20
784/784 [==============================] - 62s 79ms/step - loss: 0.1947 - accuracy: 0.9109 - val_loss: 0.1783 - val_accuracy: 0.9177
Epoch 6/20
784/784 [==============================] - 63s 80ms/step - loss: 0.1771 - accuracy: 0.9204 - val_loss: 0.1696 - val_accuracy: 0.9252
Epoch 7/20
784/784 [==============================] - 63s 80ms/step - loss: 0.1665 - accuracy: 0.9275 - val_loss: 0.1627 - val_accuracy: 0.9247
Epoch 8/20
784/784 [==============================] - 64s 81ms/step - loss: 0.1549 - accuracy: 0.9336 - val_loss: 0.1475 - val_accuracy: 0.9303
Epoch 9/20
784/784 [==============================] - 62s 79ms/step - loss: 0.1406 - accuracy: 0.9397 - val_loss: 0.1251 - val_accuracy: 0.9456
Epoch 10/20
784/784 [==============================] - 62s 79ms/step - loss: 0.1328 - accuracy: 0.9439 - val_loss: 0.1332 - val_accuracy: 0.9410
Epoch 11/20
784/784 [==============================] - 62s 79ms/step - loss: 0.1294 - accuracy: 0.9455 - val_loss: 0.1159 - val_accuracy: 0.9554
Epoch 12/20
784/784 [==============================] - 62s 79ms/step - loss: 0.1188 - accuracy: 0.9500 - val_loss: 0.1467 - val_accuracy: 0.9354
Epoch 13/20
784/784 [==============================] - 62s 79ms/step - loss: 0.1121 - accuracy: 0.9536 - val_loss: 0.1017 - val_accuracy: 0.9582
Epoch 14/20
784/784 [==============================] - 62s 79ms/step - loss: 0.1088 - accuracy: 0.9548 - val_loss: 0.1103 - val_accuracy: 0.9558
Epoch 15/20
784/784 [==============================] - 62s 79ms/step - loss: 0.1015 - accuracy: 0.9593 - val_loss: 0.0867 - val_accuracy: 0.9661
Epoch 16/20
784/784 [==============================] - 62s 79ms/step - loss: 0.0946 - accuracy: 0.9625 - val_loss: 0.0925 - val_accuracy: 0.9596
Epoch 17/20
784/784 [==============================] - 62s 79ms/step - loss: 0.0971 - accuracy: 0.9621 - val_loss: 0.1303 - val_accuracy: 0.9396
Epoch 18/20
784/784 [==============================] - 62s 79ms/step - loss: 0.0893 - accuracy: 0.9638 - val_loss: 0.0830 - val_accuracy: 0.9679
Epoch 19/20
784/784 [==============================] - 62s 79ms/step - loss: 0.0834 - accuracy: 0.9658 - val_loss: 0.0985 - val_accuracy: 0.9661
Epoch 20/20
784/784 [==============================] - 62s 79ms/step - loss: 0.0823 - accuracy: 0.9666 - val_loss: 0.1069 - val_accuracy: 0.9679
모델 평가
(test_loss, test_acc) = model.evaluate(x_test, y_test, verbose=2)
print('\n테스트 정확도:', test_acc)
269/269 - 4s - loss: 0.0941 - accuracy: 0.9681
테스트 정확도: 0.9681432247161865
plt.figure(figsize=(12,4))
plt.subplot(1,2,1)
plt.plot(history.history['loss'], 'b--', label='loss')
plt.plot(history.history['val_loss'], 'r', label='val_loss')
plt.xlabel('Epochs')
plt.grid()
plt.legend()
plt.subplot(1,2,2)
plt.plot(history.history['accuracy'], 'b--', label='accuracy')
plt.plot(history.history['val_accuracy'], 'r', label='val_accuracy')
plt.xlabel('Epochs')
plt.grid()
plt.legend()
plt.title(f"Rotating_body test accuarcy: {test_acc}", loc='left', fontdict = {'fontsize' : 15})
plt.show()
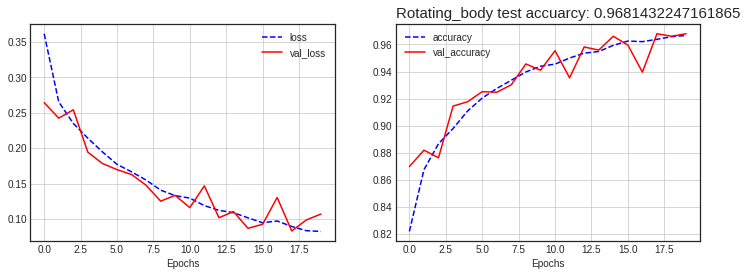
import random
random_list = random.sample(range(y_test.size), 5)
fig = plt.figure(figsize=(15, 15))
grid = ImageGrid(fig, 111, nrows_ncols=(1,5), axes_pad=0.05, share_all=True, cbar_mode='single')
y_predicted = (model.predict(x_test) > 0.5).astype("int32")
i = 0
for ax, im in zip(grid, [x_test[random_list[0]], x_test[random_list[1]], x_test[random_list[2]], x_test[random_list[3]], x_test[random_list[4]]]):
ground_truth = 'anomaly' if y_test[random_list[i]] == 1.0 else 'normal'
predicted = 'anomaly' if y_predicted[random_list[i]][0] == 1.0 else 'normal'
color = 'g' if ground_truth == predicted else 'r'
ax.set_title(f"Index : {random_list[i]}\n\n", loc='center')
ax.set_title(f"Ground_truth : {ground_truth}\nPredicted : {predicted}", loc='left', color=color)
im = ax.imshow(im, cmap='gray', origin='lower', vmin=-1., vmax=1.)
i = i+1
grid[0].get_yaxis().set_ticks([])
grid[0].get_xaxis().set_ticks([])
plt.colorbar(im, cax=grid.cbar_axes[0])
ax.cax.toggle_label(True)
plt.show()
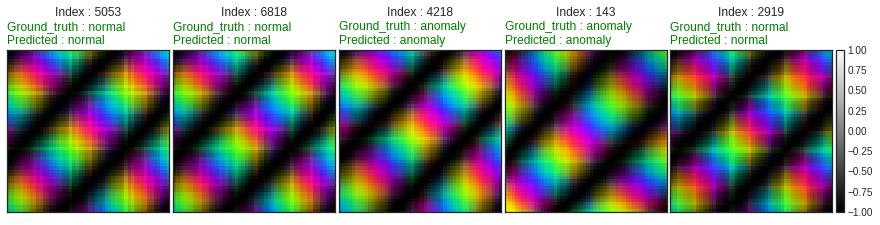

댓글남기기